概述

因为最近需要用到图卷积网络，所以需要对图神经网络做一个了解，之前也老听说GNN，GCN啥的，但是一直没有深入了解，借此机会，深入学习和理解了一下。

图神经网络涉及的内容非常多，我也不可能面面俱到，这篇文章也不打算做全面科普和讲解的目的，而是把自己的一些理解总结出来，至于很多在网上可以查到的资料，我只给出引用即可，不深入讲解，除非觉得有必要。

文章，主要是讲讲一下内容：

图、图神经网络的基本概念
图上如何做卷积和池化
卷积的两种：频谱卷积和空间卷积
常见的图卷积网络（注意不是图神经网络，那个范畴更大，我用不到，暂时也不做深入研究）
给出我收集的资料

图

先给定一个图的基本概念：

$G=(V,E,W)$

V 是节点（vertex）集合，其中节点用一个d维向量表示，$n=|V|$
X 是节点的向量矩阵，就列就是一个节点的表示，$X \in R^{n \times d}$
E 是边（edge）集合
W 是邻接矩阵（方阵），矩阵里的值，就是边的权重，$W \in R^{n \times n}$

可以把每个节点当做是一个信号（看，和信号处理勾稽上了）。

图神经网络的用途

好，有了图的基本概念，我们就会想，能拿拿图干嘛？

一个网络，我最终给这个网络一个分类
一个网络，我对网路中的每个节点进行分类（社交网络中的标签分类）
一个网络，我通过局部网络的结构（已知的标注网络）学习出另外部分的网络结构（如预测一个节点和别人的链接情况）（是否用来做OCR布局分析？）
还可以和GAN结合，用于生成一个网络结构（分子制药生成分子式）

你可以看出，其实主要焦点是在整体，还是个体上，整体就是整个大网的表示学习，个体就是每个节点的表示学习，我目前关注GNN，就是想把它应用到OCR的布局分析中，比如把bbox（识别的文字框）当做一个个的节点vertex，然后看他们彼此的关系如何？也就是有无链接？他们自己是什么分类？这样，我就能找出哪些bbox是标题，还是值，他们是否在一行，等等，这样的业务含义，从而满足商业需求。

图卷积

一个图，如何做特征抽取，我们自然而然就想象到过去我们最擅长的卷积神经网络（CNN）：

类比CNN

咱们学习CNN，先通过表示学习，学习出图的内在特征，然后用它做分类啥的。是的，没错。你为何会有这么一个思路，因为这个思路就是你过去CNN图像卷积神经网络的思路啊，把图像的特征抽取出来，然后做分类啥的。

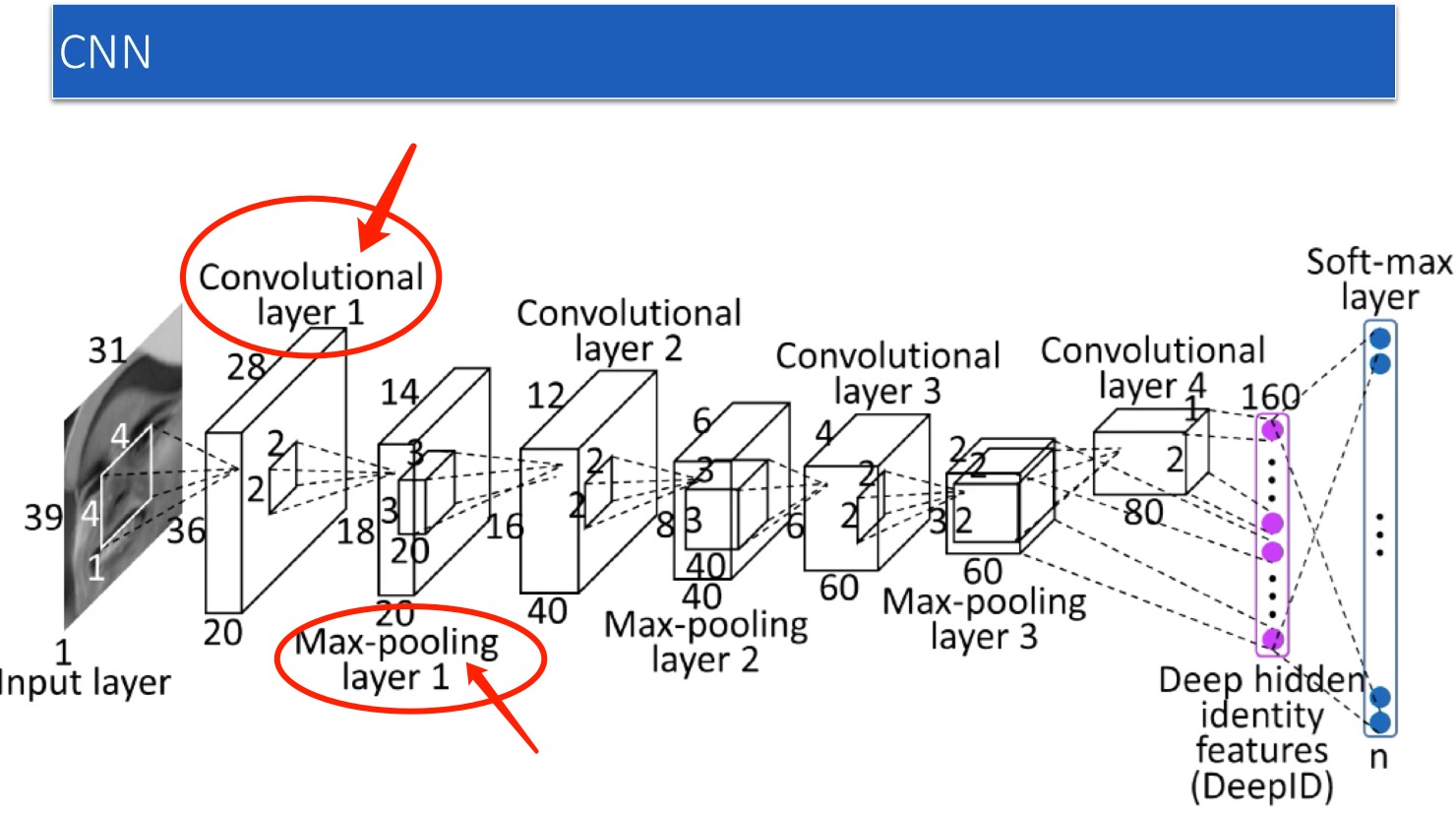
好，我们看CNN，我们的两大法器就是卷积和池化，当然核心是卷积，那么这套思路是不是可以套到图神经网络上呢？

答案是，可以的，如下图，图上也可以做卷积完成特征抽取，然后做池化，缩小网络结构，当然，不是说的那么简单，这个后面我会逐一解释，这里先直观有个印象即可。

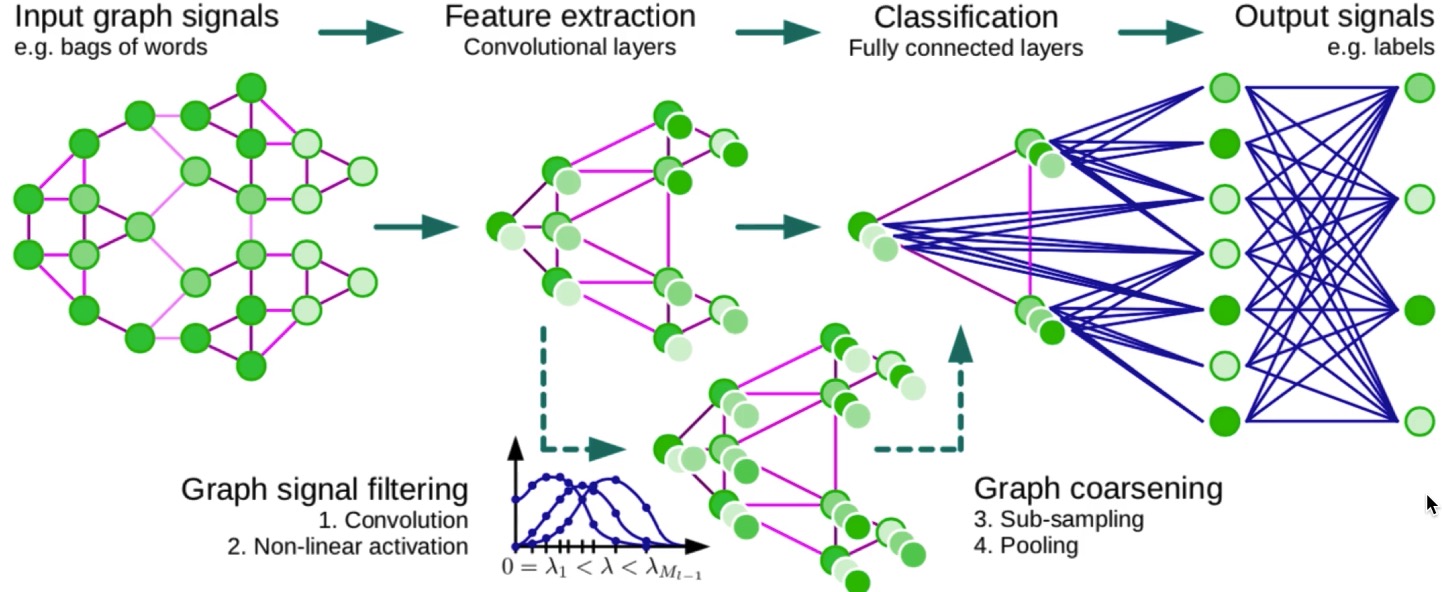
这里，我自己有个疑问，也算是给自己挖个坑：在做卷积的时候，网络中变化的是什么？是每个节点上的表示么？表示的维度为变么？网络的结构会在变么？我知道池化肯定会变的，这种先不考虑呢？我说的变是整个结构都发生根本变化。这些问题，我提给自己，未来自己来把坑填上。

接下来说说卷积，

CNN只适合欧式空间，比如图像。而基于图（Graph）GNN更通用，适合非欧空间（啥叫欧式空间，就是支持距离公式的空间。）可是，现在，我还是需要做卷积、池化，我改如何做？

现在问题变成了：图神经网络最核心的就是要解决卷积的问题，卷积最核心的就是卷积核如何确定。

先说说卷积

在讨论图（Graph）如何做卷积之前，我们有必要讨论一下，究竟什么是卷积？

本质上卷积核，是对在过滤不同频率的信号。参考。你看卷积公式$h(t) = \int_{+\infty}^{-\infty} f(\tau)g(x-\tau) dt$，

参考：视频22分钟处。

对应上图：$f(\tau)$就是右侧那个下降函数，$g(x-\tau)$是方波函数，而卷积结果（是个以时间$\t$为变量的函数）是左侧那个上升函数
$h(t)$是一个以$t$为变量的函数，是的，他是个时间函数
设想某个$t=t_0$，$h(t_0)$就是那上图中黄色面积
这个面积是一个积分，是$\tau$从$-\infty ~ +\infty$的积分，上图上，就是黄色的面积

那么问题又来了，卷积有啥用？

其实，卷积本质是为了在频域空间的不同频率信号的过滤，原因是，时域卷积=频域相乘，这个是傅里叶变换的结论，细节我会在傅里叶变换的博文中详解，这里只知道结论就可以。你用一个滤波器函数$g(x)$去和你的目标函数$f(x)$做卷积，就相当于是把他们放到了频率里，进行相乘，相乘的结果，就相当于在频率里把某些频段的值给“乘”掉了（理解这个可以参考下面参考问斩各种的方波滤波器的概念），只剩下了你所需要的频段的信号了。

时域卷积=频域相乘，卷积核本质上是一个二维函数，有对应的频谱函数，因而可以看成某种『滤波器』

参考

那么，把这个概念扩展到二维函数上，也就是图像上，图像可以看做是一个二维离散函数。图像上的分类，其实就是图像上的信号处理。那么我们来对应一下卷积的概念。 $f(x)和g(x)$的x，对应整个图像的二维位置（x，y），$f(x)$对应图像的值，$g(x)$就是对应的卷积核，时间$t$对应的就是卷积目标feature map上的一个点。你的卷积核，一个一个位置的挪动，就是在计算目标函数$h(t)$。看看，都对应上了吧！

可是，我们又要想，为何要做图像的卷积？

答案是，为了提取图像不同频率的信息。啥？！图像又不是波，怎么会有频率？有的！图像实际上可以看成是一个由不同的点上的值变化，所组成的一个东西。不同的点（二维），对应不同的值，这就是一个函数啊。既然是函数，就可以按照傅里叶变换，变换到频率里。这么说的太数学化，不好懂。你可以换个思路理解，就是像素间变化剧烈，比如从红色突然变成了白色，或者从255的值，突然变成了0，这种变化多剧烈啊！这就是高频啊。反之，就是低频啊。

图上的卷积

（注：以下理解均来自这篇很赞的图卷积的知乎解释贴，感兴趣的可以参照阅读。）

图片上可以做卷积（CNN），我们理解了，那么问题又来了？一个图（Graph）上，如何做卷积？

前面我们说了，卷积，其实就是一种滤波器，就是把图像变换到频域，然后用某个卷积核来过滤出某个频段的特性。那么，我们同样的思路，把图上的信息，变换到频域里面，然后在里面做相乘，从而过滤出某个频段的信息。这种思路就是频域卷积，论文里都称作谱域卷积（spectral domain）。

当然，我们还可以沿袭CNN的思路，但是和CNN不同，图上不具备欧式空间的平移不变性，那该如何在空域（或者说时域）上做卷积呢？这个正是空（间）域卷积（spatial domain/vertex domain）研究的内容。

谱域卷积

初始概念

最早的图卷积，是杨力昆（Yann LeCun）老师的团队们2014年就琢磨出来的，很诡异的频域卷积：

原始论文: Bruna - Spectral Networks and Locally Connected Networks on Graphs

【1、图上的拉普拉斯分解】

图上的拉普拉斯，

$L=D - W$

W上面提到了，就是边上的权重，是一个对称方阵，$W \in R^{n \times n}$
D呢？我看很多文章是都说图的节点的度的对角阵，但是实际上D的定义是：$D_{ij}= \sum_j W_{ij}$。

这里不得不说一下，网上的狠多文章都是不考虑边权重的图，或者说，权重是1，但是如果是边带不同权重的，就需要用上述公式来确定矩阵D，即一个边出度上的边的权重之合。

拉普拉斯矩阵是对称阵，所以是半正定的，所以特征值都是非负的，所有有n个线性无关的特征向量。拉普拉斯的特征值分解，通过相似对角化，就可以得到一组基：

通过相似对角化，得到的一组特征向量彼此都是彼此正交的，你可以认为是一组正交基。用它就可以表达一个新的坐标系出来，

拉普拉斯矩阵正交分解后：

\[L = U \begin{pmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_n \end{pmatrix} U^T\]

【2、图上的频域傅里叶变换】

你可以把这组由特征向量构成的正交基，类比成傅里叶变换中的不同频率，也就是不同的基，通过这组基，就可以把时域，（论文里有时候叫vetex domain）转化到频率空间里面去（spectrum domain），然后在频率里做卷积，也就是滤波，滤完后，在变换回时域（vetex domain）。

类比傅里叶变换：

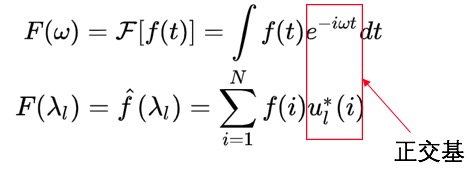
$f$是Graph上的N维向量
$f(i)$就是第$i$个节点的向量表达
$u_l(i)$就是第$l$个特征向量的第$i$维度的值
$\hat f(\lambda_l)$，就是到了频域后，这个频率$\lambda_i$对应的值。

【3、频域上的卷积】

上面只是说，图上如何做频域（spectrum domain）和时域（vertex domain）的转换，但是，其实对我们更重要的是卷积。

我们现在需要在频域内，设计卷积核通过这个卷积核的学习，可以让你学习出最优的对时域（vertex domain）中每个节点的向量表达，用这些向量表达，就可以完成分类，或者关系预测啥的了。

具体怎么做呢？

我们假设我们的卷函数在时域内叫$h$（卷积核叫啥$h$啊！TMD，论文就这么叫的，我们也叫把，一般h都表示隐层啊），是个n维度向量，和节点的向量表达维数已知。

然后我们也要把这个$h$变换到频域里去，用上面的一样的方法：$\hat h(\lambda_l)=\sum_{i=1}^N h(i)u_l(i)$

这样，我们的原始数据特征变换到频域的$\hat f$，和刚刚变换到频域的卷积核$\hat h$，可以做卷积了。

我们上面先说说卷积已经讨论过了，时域上的卷积，就相当于频域的点积，所以，卷积这个操作就变成了：

$\hat f \odot \hat h = U^T f \odot U^T h $

$\odot$ 是Hamada积，表示逐点相乘

如果再变换回去，就需要再乘以$U$，所以整个卷积过程便是：

$(f*h)_G = U( (U^T f) \odot (U^T h))$

【5、迭代起来】

你用图上的节点们的表示$h_i$，做了一个卷积（是在频域里做的），你考虑了图的结构（就是那个$U$，他是通过邻接矩阵、出入度得到的），可是，这个只是做了一次卷积。

过我们过去要用多个卷积核，卷完一层，再卷一层，变成有给深层网络，对吧？那么这里，图卷积，如何和这个形式对照起来呢？

多参数，我觉得好像是没有，这个网络里，就一组参数，就是$g_\theta$
多层网络，这个有，就是学完后，每个节点上的隐含表达更新了，那下一轮再重复这个过程，我理解就算是“下一层”了
如何更新参数？还是梯度下降啊，那也必须得有损失函数loss啊。这个，肯定是要依赖于下游任务了，比如节点分类，节点关系预测啥的。

这里有个小地方，必须得说一声，否则后面ChebNet的时候就该搞不清楚了：

为什么卷积核是一个有N（节点数）个参数的对角阵？

$h$是卷积核，对吧，长啥样？其实不用关心，因为卷积，不像之前的CNN（是在时域上做的），现在变到了频域上去了，所以你现在应该关心的是，频域上的卷积核长啥样？

它的本来面目，还记得不？是$(U^T h)$，对，就是这个样子，其实，就是一个N维度的向量，对吧？

他然后要和$f$（原始数据）做$\odot$：$U( (U^T f) \odot (U^T h))$，对吧？

好，那我直接把他从一个N维向量，变成一个$N \times N$的矩阵，然后$\odot$操作，就可以写成矩阵乘法啦。

所以，现在卷积核，就变成一个对角阵了。

好！我们终于解释了我们自己提出的问题，“为何是个对角阵？”：是因为，我们把$\odot$操作变成了矩阵乘法。别看这个问题小，愚笨的我还是想了半天才想明白的。

然后，这个$(U^T h)$，实际的长相是：

\[\begin{pmatrix} \theta_1 & & \\ & \ddots & \\ & & \theta_n \end{pmatrix}\]

对，就是这个样子，这个就是参数，是神经网络要去学习的东东。

这里再絮叨一句，这个卷积核，后来在ChebNet的时候，被诡异、神奇、创新的替换成了特征根$\lambda_i$的切比雪夫多项式了

【4、可以深度学习了】

上面的式子里，$h$是我们的卷积核，就是我们要学习的参数，终于可以用个深度网络来学习这些参数了。

不过，原始论文里，

他做法更粗暴的，直接把$U^T h$ => $g_\theta$，原有的式子也变成了：

$(f*h)_G = U( g_\theta \odot (U^T h))$

然后，最后再放一个非线性变换，就是最后的神经网络的前项公式了：

$(f*h)_G = \sigma( U( g_\theta \odot (U^T h)))$

【它的问题】

这个方法有很多很多问题，比如：

他得要求这个Graph节点数不能变，因为上述公式中的$U$是特征向量，你的节点一变，拉普拉斯矩阵就变了，你的$U$就得重新求了
你学的参数$g_\theta$，是个N维度，跟你节点数一样的啊，你节点数一遍，参数个数都得变啊
还有，这个卷积核$g_\theta$是跟整个图相关的，原因是它和整个图的特征分解相关啊，这样，他也不是局部化的，你说非局部化有啥不好？我理解是，你没法像传统CNN那样，通过一个小卷积核，通过局部的卷积操作，可以学出整个图的特征。

不好，不好那就改吧，这就引出了ChebNet，切比雪夫图网络：

改进

还记得上面说过吧，现在参数，是这个样子：

\[g_\theta = \begin{pmatrix} \theta_1 & & \\ & \ddots & \\ & & \theta_n \end{pmatrix}\]

ChebNet，来了个神奇的操作，把$g_\theta$变成了关于特征值n次$\lambda_i$的多项式：$g_\theta(\Lambda)$

\[g_\theta(\Lambda) = \begin{pmatrix} \sum_{j=0}^K \theta_j \lambda_1^j & & \\ & \ddots & \\ & & \sum_{j=0}^K \theta_j \lambda_n^j \end{pmatrix}\]

即：$g_\theta(\Lambda)=\sum_{j=0}^K \theta_j \Lambda^j$，你说这个K是啥？其实就是拍脑袋定的一个超参，他在后面推导出来的结论里有体现，即某个节点的K个hop的邻居的，具体是拉普拉斯矩阵$L^K$体现出来的。

注：利用了对角阵N次方等于对角线元素的N次方的性质。

好，接下来，骚操作来了：

卷积：

\[(g_\theta * x)=> \\ U\sum_{j=0}^K \theta_j \Lambda^j U^T x \\ = \sum_{j=0}^K \theta_j (U \Lambda^j U^T) x \\ = \sum_{j=0}^K \theta_j (U \Lambda U^T)^j x \\ = \sum_{j=0}^K \theta_j L^j x \\\]

这么改进后，不用做特征值分解啦，啦啦啦啦啦啦啦，$L$是拉普拉斯矩阵。

牢记原始谱方法的两个问题：

特征分解、特征向量求取麻烦

卷积核是全局相关的

ChebnetNet

【参考】

Chebyshev多项式作为GCN卷积核 <– 清博小哥哥superbrother讲的最好！
回顾频谱图卷积的经典工作：从ChebNet到GCN
切比雪夫显神威—ChebyNet

先自己给自己提了一个问题，“为什么要用切比雪夫多项式？这个多项式替换了啥？”

我先提纲挈领地自问自答一下：

既然上面创新性的用一个特征值n次多项式替换了参数，

ChebNet，来了个神奇的操作，把$g_\theta$变成了关于特征值n次$\lambda_i$的多项式：$g_\theta(\Lambda)$

咱先把目标列出来：

得降维吧！过去图多大，参数$g_\theta$就多少维度，不好！现在咱们得想办法给他降到一个固定的低维。
别全局相关，最好只考虑局部的特征就能学出全图来，这样，我不用全图信息，也能学出全图，比如通过采样啥的

来吧，我们搞搞看：

切比雪夫多项式

有必须要先学习一下切比雪夫展开式！参考：视频，文章

我的理解是：他是一个借助$cos,argcos$，得到的一个多项式展开方法，这个多项式有一些神奇的特性，可以被用来解决最值问题啥的。

稍微推导一下切比雪夫多项式的由来：

他尝试展开$cos(\theta)，cos(2\theta)，cos(3\theta)，… $

他观察到，展开式都是：$\sum Acos^n(\theta)$ 的样子，也就是$cos(\theta$的n次方，和前面有个系数$A$:

\[cos(\theta) = cos(\theta) \\ cos(2\theta) = 2cos^2(\theta) -1 \\ cos(3\theta) = 4cos^3(\theta) - 3cos(\theta) \\ cos(4\theta) = 8cos^4(\theta) - 8cos^2(\theta) + 1\]

然后，可以观察猜出（当然人家老人家也证明了）：

最高项的系数，也就是$cos(4\theta) = 8cos^4(\theta) …$中的这个$8$，是$2n-1$，这里$n=4$.

接下来，做一个变形，令$x=cos(\theta)，x \in [-1,1]$，也就是$\theta=arc cos(x)$，切比雪夫余弦展开，就变成了一个多项式展开了：

\[g(x) = cos(\theta) = cos( arc cos(x)) \\ g(x) = cos(2\theta) = cos( 2arc cos(x)) \\ g(x) = cos(3\theta) = cos( 3arc cos(x)) \\ g(x) = cos(4\theta) = cos( 4arc cos(x))\]

这里$g(x)$就表示，是一个$x，x \in [-1,1]$的多项式，现在x就是$cos(\theta)$啊。

然后，然后我们得到了一个$g(x) = cos(n arc cosx)$，这个$g(x)$形式上就是一个$x$的多项式，这个多项式背后，就是一个$cos(x)$的展开式。

它还有个神奇特性，就是可以高阶多项式，可以通过低阶多项式，递归推出，比如$cos(3\theta)$可以通过$cos(2\theta)$推出，而$cos(2\theta)$又可以由$cos(\theta)$推出，对应到多项式也是一样的，g_n(x)，也就是最高项为$x^n$的多项式，可以由$x^{n-1}$的多项式递归推出，具体的公式如下：

Chebyshev多项式的递推公式: $g_{n+1}(x) = 2xg_n(x) - g_{n-1}(x)$

那么，接下来，我的问题是：为何要用这么一个诡异的多项式，去替换GCN中的$g_\theta$参数？说实话，我真心没懂，是因为一组正交基的组合，可以通过多项式去拟合么？我偶然看到说，切比雪夫多项式是“以递归方式定义的一系列正交多项式序列”，难道说，这里的特征向量，就是一组正交基，他们的线性表达，恰好可以被这样的多项式可以逼近？不知道，好希望有人能给我讲讲啊。

后来看到这篇，多少给出了一些答案：

$p(x) = \sum_{n = 0}^{3} a_nT_n = a_0 T_0(x)+a_1 T_1(x)+a_2 T_2(x)+a_3 T_3(x)$，

$p(x)$是我们造出来的最高项为3次方的多项式，去拟合题目中给的4个点$(1,1),(2,3),(3,5),(4,4)$，把$x$带入进去，就可以递归的推出$T_i(x)$，结果$y$你也知道，剩下的就是解一个线性方程，求出这些待定系数$a_i$了。

也就是说，你用切比雪夫多项式，去逼近你的那些需要拟合的点。为何要这么样做呢？因为这样的拟合可以防止龙格现象，且，这样的逼近是一个“多项式在连续函数的最佳一致逼近”（其实这个我也不太懂？难道是说，这样的逼近方法最优？算了，先不研究了，继续…）

好吧，我假装，我对这里面的关系和原理已经深刻理解了（未来会的，哈哈哈），那么，我接下来看，如何应用切比雪夫多项式展开，到GCN的优化当中去吧！

前戏有点多哈…….

ChebNet

回忆一下，$g_\theta(\Lambda)=\sum_{j=0}^K \theta_j \Lambda^j$，这个是之前，骚操作，生生憋出来的神经网络参数：$g_\theta(\Lambda)$。

现在

$g_\theta(\Lambda)=\sum_{j=0}^K \theta_j \Lambda^j \rightarrow \sum_{j=0}^K \theta_j T_k(\hat \Lambda)$

这样做完，会有啥影响呢？我们来回忆一下，当初这个$g_\theta$怎么创造出来的：

ChebNet，来了个神奇的操作，把$g_\theta$变成了关于特征值n次$\lambda_i$的多项式：$g_\theta(\Lambda)$

\[g_\theta(\Lambda) = \begin{pmatrix} \sum_{j=0}^K \theta_j \lambda_1^j & & \\ & \ddots & \\ & & \sum_{j=0}^K \theta_j \lambda_n^j \end{pmatrix}\]

看，每一项，其实都是一个关于$\lambda_i$的K次多项式：$g(\lambda_1) = \theta_1 \lambda_1 + \theta_2 \lambda_1^2 + \theta_3 \lambda_1^3 + … + \theta_K \lambda_1^K$，这个是一个多项式函数，对吧？现在，我再来个骚操作，就是我用一个切比雪夫多项式，去逼近这个多项式函数：

\[g(\lambda_1) = \theta_1 \lambda_1 + \theta_2 \lambda_1^2 + ... + \theta_K \lambda_1^K \rightarrow \\ = \theta_1 T_0(\lambda_1) + \theta_2 T_0(\lambda_1^2) + ... + \theta_K T_0(\lambda_1^K) \\ T_i(\lambda_1) 就是切比雪夫递归式项\]

这个只是$lambda_1$，我们对整个$Lambda$做变换：

\[(g_\theta * x) \\ = U \sum_{j=0}^K \theta_j \Lambda^j U^T x \\ \approx U \sum_{j=0}^K \theta_j T_j(\Lambda^j) U^T x \\ 因为Chebyshev多项式作用在对角矩阵上，不会影响矩阵运算\\ 那就改变一下运算顺序，先把矩阵运算放进去 \\ = \sum_{j=0}^K \theta_j T_j (U (\Lambda^j) U^T) x \\ = \sum_{j=0}^K \theta_j T_j (L) x \\\]

OK! 现在再观察这个式子：$(g_\theta * x)=\sum_{j=0}^K \theta_j T_j (L) x$，$L$是已知的，而$T_j(L)$，也可以递归推出，那剩下的就是需要梯度下降求解的参数$\theta_j$了，而且，计算复杂度也降下来了，只要递归推一下$T_j$既可以，是$O(n)$复杂度的了。

这里，其实是有纰漏的，你如果看superbrother的推导，他的结果是：$(g_\theta * x)=\sum_{j=0}^K \theta_j T_j (\hat L) x$，注意到了么？拉普拉斯矩阵从$L$变成了$\hat L$，这个$\hat L$是什么鬼？

原因是出在，切比雪夫展开，要求$x$的定义域必须是$[-1,1]$，为了满足这一点，要让$\lambda$们的值，都要在这个范围内，要对矩阵$\Lambda$做变形：

\[\hat L = \frac{2}{\lambda_{max}} L - I\]

其中最大特征值$\lambda_{max}$可以利用幂迭代法（power iteration）求出，具体我也没去深究了，感兴趣，可以看看superbrother给出的链接。

参考切比雪夫递推式：

Chebyshev多项式的递推公式: $g_{n+1}(x) = 2xg_n(x) - g_{n-1}(x)$

可以得到：

\[T_0(\hat L) = I \\ T_1(\hat L) = \hat L \\ T_j(\hat L) = 2T_{j-1}(\hat L) - T_{j-2}(\hat L)\]

崩溃了么？

如果没有，强！我稍微总结一下：

我们要模仿CNN的卷积，为何我们要做卷积呢？我们是为了做不同信号的滤波。
可是图网络不具备空间不变形，所以呢，只好把卷积核设计到了频域里。参照傅里叶变换，我们用拉普拉斯矩阵的特征向量，当我们的正交基，来做变换。
这样下来，需要做特征值分解，且，卷积核不具备局部性，只好改进。
改进的方法是先生生憋出一个基于特征值的多项式，来替换频域的参数$\theta$
然后，在进一步，用切比雪夫多项式，来逼近这个特征值的多项式

至此，完成了图神经网络最核心的频域的骚操作，终于让基于频（谱）域的图卷积得以实现了。

GCN

你以为完了么？骚年，天真的很呐！还要简化，简化到死！这次是对切比雪夫多项式再简化，只取，0阶和1阶的展开。参考：Graph Convolutional Networks：从卷积到GCN，论文:《Semi-Supervised Classification with Graph Convolutional Networks》。

这个便是GCN的来历，不够我吐槽一下，这个名字有些无耻，因为所有这些方法其实都是图卷积（Graph Convolutional Network），人家都没好意思占用这个“大名字”，你居然就注册成商标了，呵呵。

正如上面说的，还要简化，我们一起来推导：

\[(g_\theta * x) = \\ \sum_{j=0}^K \theta_j T_j (L) x \\ \approx \theta_0 x + \theta_1(\hat L) \\ = \theta_0 x + \theta_1(\hat L) \\ = \theta_0 x + (\frac{2}{\lambda_{max}} L - I) x \\ \lambda_{max} \leqslant 2(这个我也没深究，是可以证明的) \\ \approx \theta_0 x + \theta_1(L - I) x \\ = \theta_0 x + \theta_1(L - I) x \\ = \theta_0 x + \theta_1( D^{- \frac{1}{2}} W D^{-\frac{1}{2}} ) x \\ 这个是拉普拉斯矩阵的对称归一化的拉普拉斯矩阵 \\ 然后，再简化一下，令\theta_0 = -\theta_1，上式继续简化，\\ = \theta(I_n + D^{-\frac{1}{2}} W D^{-\frac{1}{2}} ) \\ 由于谱半径[0,2]太大，归一化一下（为何做这步？没搞明白）\\ = \hat D^{-\frac{1}{2}} \hat W \hat D^{-\frac{1}{2}}\\ 其中，\hat W = W + I_n, \hat D_{ij} = \sum_j \hat W_{ij}\]

最终，

我们得到：$\underbrace{g_\theta * x}_{\mathbb R^{N \times 1}} = \theta( \underbrace{ \hat D^{-\frac{1}{2}} \hat W \hat D^{-\frac{1}{2}}}_{\mathbb R^{n \times n}} ) \underbrace{x}_{\mathbb R^{n \times 1}}$

这里有一些需要说明的，$x$居然是$n$维度的，$n$是节点数，出乎意料把，这个原因是，

参考

$x$就是graph上对应每个节点的feature构成的向量，$x=(x_1,x_2,…,x_n)$ ，这里暂时对每个节点都使用标量，相当于channel为1。

把$x$扩展到多维$C$去，$x \in \mathbb R^{N \times 1} \rightarrow X \in \mathbb R^{N \times C}$,$N$是节点数，$C$是节点上的维度表示，$X$变成整个图的特征矩阵（包含了所有的nodes）。随之参数也从$\theta \in \mathbb R \rightarrow \Theta \in \mathbb R^{C \times F}$,$F$为卷积核个数。

最终，公式表达为：

\[\underbrace{Z}_{\mathbb R^{N \times F}} = ( \underbrace{ \hat D^{-\frac{1}{2}} \hat W \hat D^{-\frac{1}{2}}}_{\mathbb R^{N \times N}} ) \underbrace{X}_{\mathbb R^{N \times C}} \underbrace{\Theta}_{\mathbb R^{C \times F}}\]

GCN已经把谱域家族荣耀到极致了，但是，他仍然是不完美的：

GCN的缺点也是很显然易见的:第一，GCN需要将整个图放到内存和显存，这将非常耗内存和显存，处理不了大图；第二，GCN在训练时需要知道整个图的结构信息(包括待预测的节点)

后面，我们来填这2个坑。

空域卷积

上面终于谈完了谱域（Spectral）卷积啦，现在我们可以说说空域（Spatial）卷积了。

空域卷积，对我们这些正常人来说，可能更好理解。就是得有个卷积核，过去是和图片卷积，现在是要和图卷积了，过去是在图片上，卷积核形状是固定的，现在是不固定的了，如何解决不固定问题，就是要解决的问题啦。当然还有池化，也是需要解决的问题。还可以引入注意力模型，恩，这些都是可以类比的了。

GraphSAGE

参考：

Inductive（归纳） learning和Transductive（直推） learning的概念？就讨厌玩概念，Inductive，就是从局部的图推演出整体的图特性，就是用图上某些有限的节点和关系，学习出整个图上泛化特性。而Transductive就得用整个图的信息才可以，前面的那一堆谱方法，都是用所有的节点，即使是最简化的GCN，也需要所有的节点信息（$\underbrace{X}_{\mathbb R^{N \times C}}$ 里的N，就表明是所有的节点）。

正如前面谈及GCN的不足的时候提及到的，很多时候，你是不可能用所有的图的节点这么折腾的，比如社交网络中10亿+的节点数，这得多少大显卡才跑的开啊。而且，你是知道邻接矩阵的的，也就是你知道这个图的所有节点间的关系。但是，现实中，很多情况，连关系可能也是要学习和探索的。

GrachSAGE（Graph Sample and Aggregate）就是为了解决GCN的上面说的两个问题：

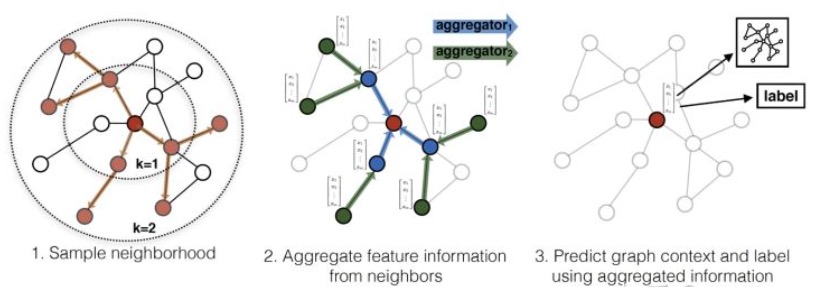
GraphSAGE是这样玩的：对每一个节点，随机采样他的K跳近邻，采样出一颗子图（其实是个树吧?），然后使用一个聚合函数（这个函数得设计），分K层依次聚合，就跟消息传递似的，一直从边缘传播到中心，更新这个节点的embeding表示。

【咋采样？】

采用一个叫“定长抽样”的方法，固定当前节点的邻居数为$S$，然后采用有放回的重采样/负采样方法达到，保证每个节点（采样后的）邻居个数一致，这样做是为了训练时候批次一样。

【这里参数是啥？】

你不是定义了K跳/层邻居（K-hop）了么？所以你就有K个参数，每个参数是应该是$\matbb R^D$，而不是个矩阵，不过应该有K个，每层一个。然后，每一个邻居，都要先和这个$W$相乘，然后聚合（聚合有3种方式，后面提），然后逐层向中心聚拢。每一层（第k层）共享一个相同的$W_k$，大家都用这一个$W$。

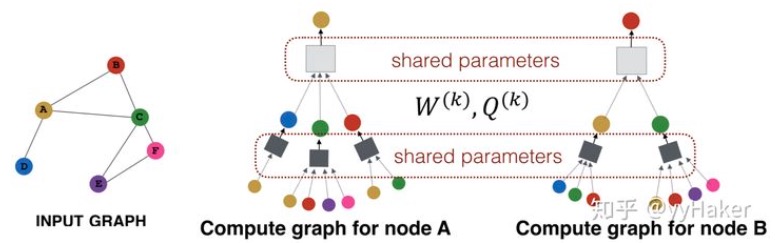
【咋聚合？参数呢？】

就是如何根据周边的节点，算出当前目标节点的更新后的embeding值。(你看，其实图结构没变)，一共有三种方式：Mean、LSTM、Pooling。（这块没细看，需要再看，大致明白就成）。

【损失函数】

如果是有监督的情况下，可以使用每个节点的预测lable和真实lable的交叉熵作为损失函数。如果是在无监督的情况下，可以假设相邻的节点的embedding表示尽可能相近。

【GraphSAGE得到了啥】

它是得到了每个node的embeding的向量，然后你可以单个取出一个向量来，去做分类、预测啥的了，每个node有个语义表示啦！

【GraphSAGE的缺点】

GraphSAGE也有一些缺点，每个节点那么多邻居，GraphSAGE的采样没有考虑到不同邻居节点的重要性不同，而且聚合计算的时候邻居节点的重要性和当前节点也是不同的。这个就需要下面介绍的GAT（Graph Attention Networks）来解决喽。

GAT

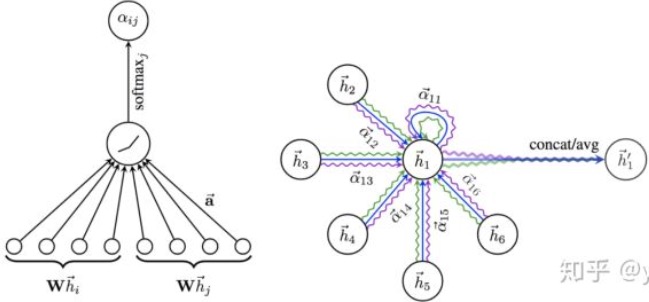
开源项目

pytorch的那个项目

开源的那个

参考

文档

精通GCN全攻略
知乎：如何理解 Graph Convolutional Network（GCN）？，超赞的讨论帖
图神经网络小结
GNN 入门系列: 直观理解和应用介绍，简单易懂的入门贴。
GNN图神经网络综述，我勒个去，这个哥们整理的太全了，基本上可以覆盖所有的网上的资料了。
知乎上一个很赞的GNN系列七篇
拉普拉斯矩阵与拉普拉斯算子的关系

视频

【目前看过的】

图卷积神经网络-沈华伟
高级人工智能第七讲-图神经网络中国科学院大学 2020秋季沈华伟，沈老师讲的最最棒。
台大李宏毅助教讲解GNN图神经网络，宏毅老师的助教也确实不同凡响，讲的还不错。
图神经网络介绍-Introduction to Graph Neural Network（GNN），不知名的台湾小哥的讲座，基本上也是GNN通识教育。
网络上的CNN-图卷积网络模型，集智的小姐姐的科普讲座，思路很清晰。
频域、谱域以及拉普拉斯算子在图上的应用，小姐姐讲的脉络很清晰，可惜没讲完。
PGL全球冠军团队带你攻破图神经网络
图网络论文读书会 18 期分享：高飞《GNN可以有多强？》集智学园:这个是一个评价GNN框架的论文的讲解。

【待学习的】

GNN图神经网络

概述

图