Batch Normalization

同事遇到一个奇怪的现象，她训练的模型看loss的表现挺好的，在验证的时候，如果同一批次的图片差异性比较大，预测出拉来的结果很好。但是，如果同一批次图片长的很像（比如就是同一图片略微变化的增强图片），预测结果就是非常不好。

她怀疑是由于Batch Normalization的问题，于是，一起对Batch Normalization进行了研究和讨论。我把讨论过程中的理解写下，便形成了这篇博客。

为何要做Normailization

首先，一个问题是，为什么要做Normalization，也就是中文所谓的“正则化”？

这个概念是来自于机器学习，我先给出结论“做正则化，是因为，这样可以防止过拟合”。

为了解释这一点，需要从模型的容量、偏差和方差的关系、过拟合欠拟合等诸多方面讨论，这里我不想展开，我给很多参考文章，里面包含了这方面的讨论，感兴趣的同学可以阅读并深入研究。

这里，我只想用比较通俗易懂的语言，来解释一下：

使用复杂（跟“$x$的高阶多项式”、“表达能力更强”、“更多的参数”、“模型容量更大”差不多都是一个意思）的模型，来去拟合数据的分布的话，特别容易过拟合；但是要是用太简单的模型，你又无法拟合出数据的真实分布。所以，你得权衡，不能太复杂也不能太简单。

一个解决的办法是，你先搞一个复杂的模型，然后再想办法去约束他。

约束的办法是，尽量通过调整参数$w$，使其变小，甚至变成0，从而是模型中的维度降低。在传统的机器学习中的L1、L2正则，就是这样的一个调整思路。

而在深度学习中，是Dropout和Batch Normalization如何。

机器学习中的L1、L2和深度学习中Dropout和Batch Normalization如何类比对应上呢？我在网上找了一些文章研究了一下，结论是：他们对应不上。

看知乎上关于L1、L2 VS Dropout和BatchNormalization的讨论，可大致理解他们彼此没啥对应关系：

神经网络中 L1 正则化和 dropout 正则化对weights 稀疏化的实质区别是什么？

L1正则化和Dropout，二者的目标不一致，一个是减少权重项，实际上是追求降低复杂度，一个是增加随机扰动构造ensemble optimization的效果，目标是追求系统鲁棒性，但本质也是一个能量约束。

dropout提出的初衷是在神经网络上模拟bagging，原理比较模糊、数学上不大明确。

关于batch_normalization和正则化的一些问题？

关于它的理论研究其实还不怎么充分。BN的计算涉及用基于mini batch计算的均值、方差代替真实均值、方差，这就起到了正则化的作用。但正则化只是BN顺带的一个作用。

所以，作为工程党，我能做的就是用L1、L2去约束常见的机器学习模型；使用Dropout和BatchNormalization去约束深度神经网络模型。

【参考】

L1、L2正则化

L1和L2的推导一直都是面试必考，大致沿着两条思路都可以推导出来：

参考这篇：深入理解L1、L2正则化：

方法1：正则化理解之基于约束条件的最优化：加上对参数$w$进行范数的约束，用$l_0,l_1$范数小于$C$来作为约束条件，利用拉格朗日算子法来解这个带条件的优化问题，就可以退出L1、L2公式。
方法2：正则化理解之最大后验概率估计：假设参数$w$属于拉普拉斯分布，就可以推导出L1；$w$属于高斯分布，就可以推导出L2正则公式。
L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0

因为L1、L2不是本篇博客重点关注的内容，这就捎带着提一下，感兴趣，可以去阅读参考中的文章，它们都已经给出了非常详细的公式推导和讲解。

【参考】

深度学习中的Batch Normalization

Dropout也是一种正则化方法，你可以通俗地理解为bagging的朴素应用，因为这篇博客主要讲BatchNormailization，这里特不想展开了。

好了，我们终于迎来了我们这篇博客的猪脚：【Batch Normalization】

为什么Batch Normalization管用

Batch Normalization的原理啥的，参考的文章们讲了一通，我还是愿意用我的大白话谈谈理解：

他们说的ICS（Internal Covariate Shift），就是说，你浅层的参数细微调整，会对后面层参数产生蝴蝶效应，导致不收敛。
ICS的根本原因，又是因为你的训练数据导致的，训练数据的每个维度上的值变换太剧烈，就会导致参数跟着调整剧烈，所以要尽量让输入的数据保持稳定，就是尽量让他们在一个尺度上
怎么保持一个尺度呢？就是通过Normailization，使得维度上值均值为0，方差为1
引入$\gamma,\beta$，说是，怕正则限制了模型的表达，给他一些弹性。不过这个是网上很模糊的说法，我尝试搜索了很多文章，都没有把这个问题讲的特别明白。

这篇《Batch Normalization详解》里面，对于$\gamma,\beta$的解释，相对清楚一些，仅供参考：

没有scale and shift过程可不可以？ BatchNorm有两个过程，Standardization和scale and shift，前者是机器学习常用的数据预处理技术，在浅层模型中，只需对数据进行Standardization即可，Batch Normalization可不可以只有Standardization呢？答案是可以，但网络的表达能力会下降。直觉上理解，浅层模型中，只需要模型适应数据分布即可。对深度神经网络，每层的输入分布和权重要相互协调，强制把分布限制在zero mean unit variance并不见得是最好的选择，加入参数𝛾和𝛽，对输入进行scale and shift，有利于分布与权重的相互协调，特别地，令𝛾=1,𝛽=0等价于只用Standardization，令𝛾=𝜎,𝛽=𝜇等价于没有BN层，scale and shift涵盖了这2种特殊情况，在训练过程中决定什么样的分布是适合的，所以使用scale and shift增强了网络的表达能力。表达能力更强，在实践中性能就会更好吗？并不见得，就像曾经参数越多不见得性能越好一样。在caffenet-benchmark-batchnorm中，作者实验发现没有scale and shift性能可能还更好一些。

怎么做Batch Normailization

好吧，理论差不多了，我们实战一下：

看例子：

上图的网络是个全连接网络，全连接网络中，如何做Batch Normalization呢？

很简单！就是对绿框中的8个数据求均值和方差，然后使用计算出来的均值和方差，来正则化每个数。

细节来了，这$\color{green}{绿框}$里的数，是一个批次（8个）的第一个维度的值，所以，你算的结果，是8个批次在第一个维度的均值和方差。

然后你还要依次计算其他维度的，最后把方差$\mu$和均值$\sigma$带入到这个公式：

$\hat{x} = \gamma * \frac{x-\mu}{\sqrt{\sigma^2+\epsilon}} + \beta$

你就可以得到每个数值被Batch Normailization之后的新值了。

当然$\gamma,\beta$是需要学习的。

那CNN如何做Batch Normailization呢？

全连接网络我们谈完了如何做Batch Normailization，那CNN网络如何做呢？

我们首先读一读这篇：

对卷积层来说，批量归一化发生在卷积计算之后、应用激活函数之前。如果卷积计算输出多个通道，我们需要对这些通道的输出分别做批量归一化，且每个通道都拥有独立的拉伸和偏移参数，且均为标量。设小批量中有 m 个样本。在单个通道上，假设卷积计算输出的高和宽分别为 p 和 q。我们需要对该通道中 m×p×q 个元素同时做批量归一化。对这些元素做标准化计算时，我们使用相同的均值和方差，即该通道中 m×p×q 个元素的均值和方差。

是的，是在每个通道上，算所有批次的一个均值和方差。

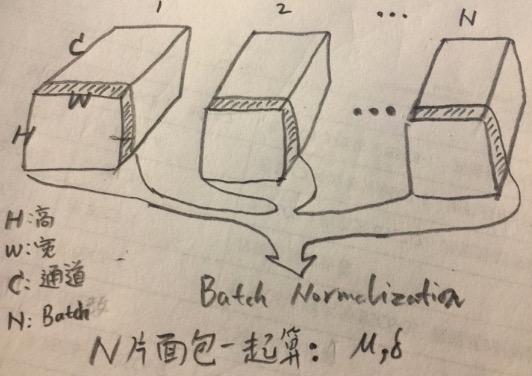
如上图，我们算均值和方差，用的是所有批次的，同一个通道里的所有的值，也就是图中所形容的，“把N个批次的面包片的数据一起来算”，这里一个面包片形容一个通道。

比如，这一层的CNN的Feature Map结果，假设其维度是[N,H,W,C]，那么，计算完成的均值$\mu$是[C]个，方差$\sigma$也是[C]个。

接下来，我们用这个通道算出的两个标量$\mu,\sigma$，对这N个面包片里面的所有的值进行归一化，得到的结果，便是Batch Normalization的结果。

训练时候和测试时候的Batch Normalization

训练的时候，需要每个批次的数据，计算$\mu,\sigma$，然后梯度下降学习$\gamma,\beta$。训练的时候，还需要记住这些均值。为什么呢？因为测试的时候需要用，这个后面会谈到。可是，这么多批次，如何都记住呢？答案是，使用移动平均法，不停的计算，每次计算后，都在网络中记录这个移动平均值。

这里有个小疑问❓训练的方差和均值，用的是这个批次计算出来的，还是移动平均出来的呢？我自己推断，应该是移动平均出来的，原因是，这样才更接近全局的样本的平均值和方差嘛。

测试的时候，由于数据量很少，你用这个批次的均值和方差来做Batch Normalization，是有失公允的，应该使用所有样本的均值和方差更合理。训练的时候，我们恰好已经记住了所有数据的全局移动平均值的均值和方差，使用它们，代入Batch Normalization公式进行计算就可以了。

所以，如何计算方差和均值，是训练和测试的时候的一个重大区别。

你自己也可以脑补，这些移动平均的均值、方差，其实跟参数类似，也是要记录在网络当中的。所以，我们甚至可以说，在Batch Normalization这个环节，参数有$\gamma,\beta,移动平均\mu,移动平均\sigma$4类。

【参考】

写在最后

好，我们已经捋了一遍了正则化、Batch Normalization了，我们来总结一下。

正则化就是为了解决过拟合问题，传统机器学习使用L1、L2正则化方式，而深度学习使用Dropout和Batch Normalization作为正则化的手段。Batch Normalization，在训练的时候，使用当前批次的均值和方差计算Batch Normalization结果，同时学习$\gamma,\beta$两个参数；而到了测试阶段，均值和方差，就要使用训练时候的全局移动平均均值和方差来计算了。

最后，让我们再回最初的同事提出的那个问题：“训练的时候，同样类型图片的预测结果不好”。对于这个问题，我们可以大胆的推测，是因为这批图片缺乏了多样性，导致他们和之前网络遇到的图片的平均值偏差太大，致使网络无法适应，导致了最终识别的效果不佳。在我看来，这其实是一个正常的现象，只要后续训练过程中，图片足够多样化，通过不断地训练，这个问题就可以被消除。当然，训练的时候，我们还是也应该避免，同一类相似图片作为一个批次，而应该让批次内的图片也尽量多样化才好。

再补充

后来，同事再次反馈，她解决了这个问题。

我对她的问题的理解，是有问题的，她之前的问题是，使用tensorflow加载后，训练的没有问题，而是在训练结束后，再预测的话，会有同样类型样本，预测正确率下降的问题。

后来，她说她解决这个问题，解决的办法是，在加载imagenet预训练模型的时候，把加载模式从训练模式，改成全部都加载的模式（即也加载每个节点上的均值和方差）：

res_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='resnet_v2_50')

改为

res_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='resnet_v2_50')

我们讨论了一下，这个原因可能是，最开始加载的resnet，如果是使用了TRAINABLE_VARIABLES标志的话，会丢掉了imagenet预训练模型中的每个节点上的均值和方差，然后在这个基础上，去训练，其实是丧失了Resnet的原本的模型的东西。然后在这个基础上训练的时候，你的每一个批次，都会从头开始计算每个节点上的均值和方差了，而网络上重新开始记录这些方差和均值的移动平均值了（包括Resnet的网络节点们）。这导致，预测的时候，这些方差和均值，已经和Resnet的Weight们，不是那么匹配了。

正确做法，应该是在加载Resnet开始训练的时候，同时加载这些节点上的均值和方差，也就是改成GLOBAL_VARIABLES标志。

同事最终也验证了这一点，去掉这个标志后，加载Resnet，然后重头开始训练，收敛后，再去测试，就没有这个问题了。