深度增强学习-DRL

转载说明

文章版权归本网站所有，所有的转载请告知作者(piginzoo@qq.com)，并在转载文章中，注明“此文章转自（www.piginzoo.com）动物园的猪”的字样，并标明本网网址，对不遵守本声明，违法、恶意使用本网内容者，本网保留追究其法律责任的权利。

日期：2019年01月10日    阅读量：

前言

深度增强学习难么？难，也不难!

不难在，没有太多的数学公式，甚至比机器学习那些算法的数学推导都少很多。

难，难在整个体系，概念，忒TM多了。不信？！你就跳到参考资料章节的“概念”里，去看看那一坨概念就明白了。

我的体会是，要搞清深度增强学习，就得先搞清楚增强学习，而增强学习里，马尔科夫决策链，贝尔曼方程，模型和非模型，预测和控制，这些核心概念都得门清。

强化学习的分类：

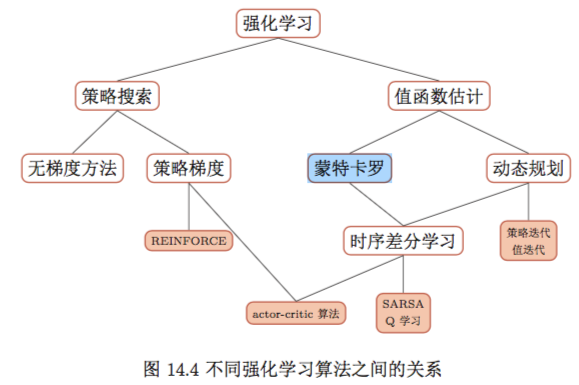
概述

增强学习reinforcement learning最核心的是学一个策略 $\pi$，然后这个策略$\pi$对某一个环境的状态s，可以给出一个action a，然后a会导致状态发生迁移，并且这个时候，环境会给出一个奖励r。整个过程就是不断地寻找这个$\pi$，找个最好的或者相对好的，从而让奖励的期望值最大。所以，大家都说，增强学习实际上是一个决策算法，帮助你做出更好的决策。

马尔科夫决策过程（MDP）

马尔科夫决策过程（Markov decision process,MDP）。它是由⟨$S;A;P;R;\gamma$⟩ 构成的一个五元组，其中：

  • S是一个有限状态集，就是你处于哪个状态啊
  • A是说采取啥动作
  • P 是状态转移概率矩阵：$P^a_{s->s′}$ ，就是你在s，采取a，那么你跳转到下一个状态的s’的转移概率
  • R 是一个奖励函数，$R_s^a = E[R_{t+1}|S_t = s,A_t=a]$，注意，是个期望哈，这个“期望”的概念很重要
  • $\gamma$是一个衰减因子: $\gamma\in$[0,1]，这个是为了让整个收益收敛。

可是，你要问了，为何会有转移概率，动作a是如何产生的? 对，好问题。动作a的产生，就是靠一个$\color{red}{策略\pi}$。有了$\pi$，他会告诉你，你当前在这个状态s，会选择哪个动作a，或者以多大概率选择动作a。

是的，总结一下，$P^a_{s->s’}$,$R^a_{s->s’}$，但是某个状态S的时候，应该采取哪个action：a，是由$a=\pi(S)$，也就是策略决定的。

$\color{blue}{画外音}$

咱强化学习，学啥啊？就是学这个策略$\pi$啊！！！你还可以把这事用个数学公式表达出来，你丫学的就$a=\pi(s)$，这个太粗暴，啥给个s就得到了个a啊，你可以温柔一点，写成 $\pi(a|s)$，这就变成了概率分布了，是s给定下的选择某个a的概率分布。恩，这个函数，或者这个概率分布，就是你学出来的$\pi$啊，这就是我们强化学习的终极目标啊。

收益（$G_t$）

从某一个状态$S_t$开始采样直到终止状态时所有奖励的有衰减的之和:

$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} … = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}$

恩，注意，$\color{red}{这个值是收敛的}$，这狠重要噢。一般来说，这个序列有完蛋的时候，所以这个数是个收敛的数，可是如果这个序列无限量呢？那么用个$\gamma$，就可以让他还是可以收敛的了。另外，这里还隐含了一个概念，是说，在t时刻，这家伙处于$S_t$状态呢。

$\color{blue}{画外音}$

干嘛攒出来这个收益，还要他收敛呢？是为了衡量咱们的策略$\pi$啊。你想啊，你总的有个量化指标来衡量你的策略牛逼么？为毛就比我的牛逼啊。那好，咱俩都用各自的策略，是骡子是马，来出来溜溜。出来比了，那总的拿个东西衡量吧，这个衡量，就靠这玩意$G_t$，到最后（终止状态），谁收益高，谁的策略$\pi$就牛逼呗。那个$\gamma$是为了让这个值收敛。

BUT，不过，但是，你注意到了么，他的视角不是游戏开头到游戏结束，他是基于某个状态的。我靠，你可能奇怪了，为毛呢？你干嘛从一个状态开始测算收益呢？恩，问的好！是因为，你丫在决策过程中的时候，你玩到半截了，你不是上帝视角，你深陷游戏当中，当局者正迷呢，“兄弟！求你就告诉我，我选a1好，还是选a2，还是选…”，好，我告诉你：你就选择，a之后，从a的那个状态开始，到最后的受益最大的那个a吧。冥冥之中，你就听到我的这个点拨，你就可以毅然决然地选择某个a，杀出重围，继续前行。其实，哪有什么冥冥，这个冥冥就是策略$\pi$啊，“理科男！信概率，别信命！”

不过，你注意到了么？这个是一次的得分噢，你玩吧，玩到哏屁，你的得分。你说“哥们，你这也太武断了把，我就玩一次，你分比我高，就说你的策略比我好，不服！”，对，你说的对，所以，咱们得取个期望，好！引出下面的“价值”，走着，继续看….

价值（Value）

对，上面胡喷的时候，有个细节你可能疏漏了。那个收益，只是从某个s开始到哏屁（死了）的一次收益，不行，太随机，所以，要！期！望！

恩，来了

$v(s)= E[G_t|S_t = s]$

马尔科夫奖励过程中状态收获$G_t$的期望，$G_t$是某个时刻在特定的$S_t$开始，往后一嘟噜决策的收益，对吧？那这玩意随机性很强啊，下次再从这个状态出发，收益可不一定一样啊，肯定是千奇百怪啊，怎么办？取期望啊！所以，就引来了$v(s)$，价值。

$\color{blue}{画外音}$

你玩吧，从某个状态s开始哈，玩到死，我给你算个分。然后，你再玩，再玩到死，又得一个分。然后你就不停的玩。玩出期望来。这个期望的分，就是你这个s的$v(s)$。玩无穷次，我靠，这不就是蒙特卡洛采样么？

注意，这个value用于是属于某个s的，来衡量你这个s牛逼不牛逼的。你说了，衡量s牛逼干嘛用呢？兄弟，你知道某个s牛逼了，你选动作a的时候，是不是应该挑选那个大招a’，让他奔着牛逼的s去啊。

价值函数（Value Function）

你说了，这个价值怎么算啊？你别告诉我用期望，一想到期望我就头大，得知道概率，得采样，balabala…，不玩了，我玩游戏去了，再见……

回来，兄弟，我有妙招，我给你个函数，你把s传进去，噗呲，这个value就出来了，妙不？

对，这个就是价值函数：

如果存在一个函数，给定一个状态能得到该状态对应的价值，那么该函数就被称为价值函数（value function）。价值函数建立了从状态到价值的映射。

啥意思呢？就是你告诉我一个状态$s$，然后我就告诉你这个期望值$v(s)$，这不就是一个函数么。恩，对，这个函数就是大名鼎鼎的价值函数。

如果状态s是离散的，可数的，你整一个表，来表示这个价值函数就可以。如果丫是连续的，无数个状态s，你咋整？就得用个函数了，甚至用个神经网络来表示了，呵呵，对吧，这里先不细讲，你体会到这个意思就成。

你又该说了，“哥们，你丫别一个劲地忽悠我，你说如果存在一个函数…，这个函数到底到底是啥？”

来，推导一下：

\[\begin{align} & v(s)=E(G_t|S_t=s) \tag{1}\\ & =E(R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} ... |S_t=s) \\ & =E(R_{t+1} + \gamma ( R_{t+2} + \gamma R_{t+3} ...) |S_t=s) \\ & =E(R_{t+1} + \gamma G_{t+1} |S_t=s) \\ & =E(R_{t+1} + \gamma v(s_{t+1}) |S_t=s) \\ \end{align}\]

来看看最后这个结论：

$ v(s) = E(R_{t+1} + \gamma * v(s_{t+1}) |S_t=s) $

这个式子，说的是，你评估$v(s)$，需要你知道你的下一个可能的迁移过去的$s_{t+1}$的$v(s_{t+1})$，乘以衰减因子$\gamma$，然后再加上系统给你的一个你调到下一个状态时候给的奖励$R_{t+1}$，算出一个期望，才是你s的价值：$v(s)$。

看晕了把，讲人话，就是说，你想评估你当前这个s的价值，得需要你后续的那些$s_{t+1}$的v值们，然后一通骚操作的求个期望，才能评估出来。

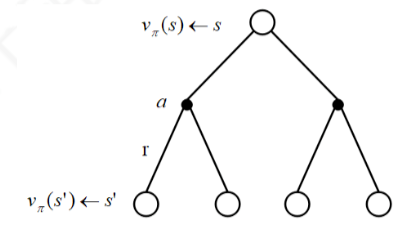
注意哈，这里有个细节，就是你评估当前状态的价值value，得用未来s的价值value，哈哈，对，就是这么变态，你问了，当前的值，我都不知道，未来的值我就更不知道了，你这不是逗我玩呢么？！对，我就是逗你玩呢，哈哈。好，不逗你你了，我想你保证，这事是可以干的，一会儿你就知道。

价值函数忒重要了，咱们啊，再换个角度看价值函数

换个角度

（其实，不是为了换个啥角度，只是因为，我之前写了一大坨，不舍得删，所以，再让你“换个角度”，再看一遍。哈哈。不过，应该是有点用的，耐心，patient！）

轨迹（τ）

这马尔可夫决策过程，可以类比打游戏。就是给定一个策略 $\pi(a|s)$，玩一个$\color{red}{轨迹(trajectory)}$，轨迹$τ$也就是你从当前状态开始玩，一直到你哏屁，这个过程叫$τ$,

$τ = s_0,a_0,s_1,r_1,a_1,··· ,s_{t−1},a_{t−1},s_t ,r_t$，我们来算算这个$τ$的概率：

轨迹概率（$p(τ)$）

\[p(τ) = p(s_0, a_0, s_1, a_1, · · · ) \\ = p(s_0) \prod_{t=0}^{T-1} \pi(a_t\|s_t) p(s_{t+1}\|s_t,a_t)\]

最后一部分，$p(s_{t+1}|s_t,a_t)$，其实就是 $\color{red}{游戏本身}$ 呀，你仔细想想，对不对，就是你当前在$s_t$，然后你做了一个action：$a_t$，然后这个概率怎么跳，是你这个agent无法控制的呀。

收益（$G_t$）

恩，在聊一遍$G_t$，跟之前的，上一节讲的，是一个东西。

对于一个$\tau$，也就是一个游戏从头到尾的一个回合来说，这个总的成绩回报是：

对于有限回合和无限回合两种：

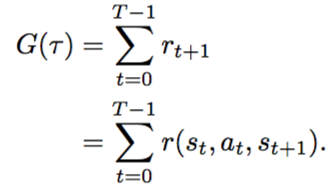
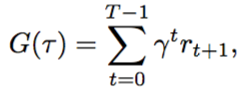
$\gamma$是折现因子，在[0,1]之间

我们上面知道了轨迹（从某状态到哏屁）概率，知道了收益（某状态开始到死的累计收敛收益），我们想干啥？我们该干啥了？

我们当然是想让这个总和回$G(\tau)$的期望最大啊：

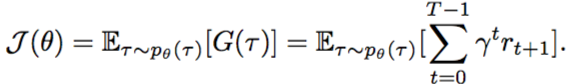
可是，为何说要求期望最大呢？因为不同的$\tau$这个值是变动的，你这么这么打，下次那么打，所以，用概率来求平均，就变成了期望。

基于模型[Model based]的策略求解

上帝视角

金山-高杨老师讲的时候，讲到一个上帝视角，挺有启发性的。

看这张图，是游戏的决策，是一个树形结构，这里是极度简化了，这张图就是假设游戏从S1出发就2步游戏就结束。恩，你是上帝，你知道所有的游戏分支，那就好办了，你评估S1的得分问题，就变成了一个树搜索问题了：

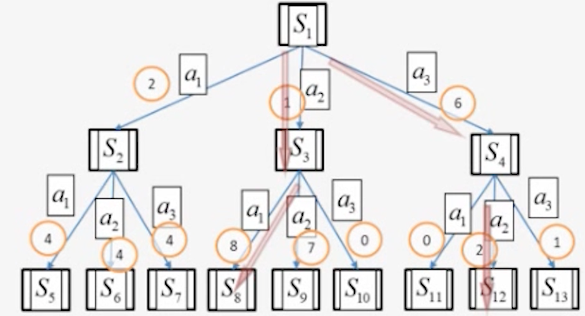
本质上，算一个$G(\tau)$是一个树搜索问题，算$V(s1)$，就是算s1的时候，最多得分是s1a1s3a1这条路。

这个是插曲哈，是为了让你理解状态的层次的感觉，这段你可以去听高杨老师的讲座，很赞，很快就能帮助理解强化学习的本质。

贝尔曼方程

好，开始说说贝尔曼方程了，

前面我们不是说了么，$v(s)$的计算：$ v(s) = E(R_{t+1} + \gamma * v(s_{t+1}) |S_t=s) $

好，我们把这个期望按照期望公式展开，即$\sum x*p(x)$：

$v(s) = R_s + \gamma * \sum\limits_{s’\in S} P_{ss’} * v(s’) $

恩，这玩意就是贝尔曼方程，看上去不好理解，其实就是个递归方程，要算的$V(S)$其实是对树往下的总得分的一个期望，他没法遍历树，就把$V(S)$表示成它的下一级S’的$V(S’)$的$\Sigma$求和。

它提示一个状态的价值 由该状态的奖励以及后续状态价值按概率分布求和按一定的衰减比例联合组成。

牢记：他是用来算一个状态价值的。是一个递归方式定义的。

$\color{blue}{看个例子}$

我给你，跳到某个状态的得分，就是R；再给你转移的概率，就是每条线上的那个概率值；你来算算圈里的值，也就是$v(s)$。

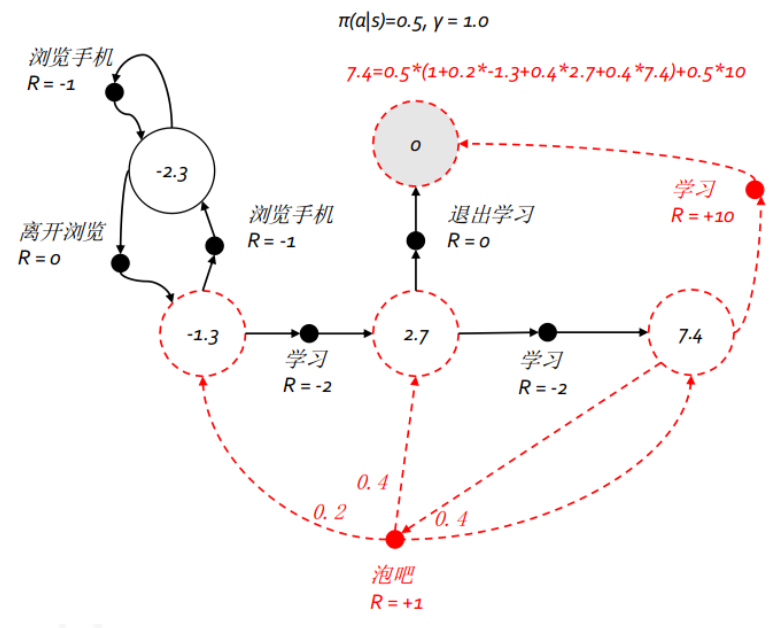
这玩意可以看成是一个方程，求解出来$v(s)$，可惜，这玩意求解计算复杂度很高（我也不知道为何？参见叶强的《强化学习》$p_10$页探讨这个问题），那咋办？没事，后续会讲别的办法来求解。

你现在可能有点晕，你朦胧着觉得，$v(s)$就是某个状态的好坏，可以算，用递归方式啥的，可是，你可能很想知道，到底这个值函数能干啥，好，我们来深入探讨一下他都能帮我们干啥：

状态价值函数$v(s)$、行为价值函数 $q_\pi(s,a)$

前面咱们讨论了价值函数了，这里再深入讨论他，并且，还要引入一个新的函数行为价值函数，Q函数。

状态价值函数$v(s)$，他其实只描述了一个状态牛逼否，他没有提及动作，可是，我们就是想知道，在某个状态s，我采取某个动作a1，我还可以采取另外一个动作a2，要是能评估从这个s，选哪个动作，可以让我一直玩到哏屁，得分的期望高呢？这个时候，就引入一个新的概念，叫$\color{red}{行为价值函数，q_\pi(s,a)}$。

$q_\pi(s,a) = E(G_t | S_t = s, A_t = a)$

按照贝尔曼方程展开，

$q_\pi(s,a) = E(R_{t+1} + \gamma q_\pi(S_{t+1},A_{t+1}) | S_t = s, A_t = a)$

再展开，

$q_\pi(s,a) = R_{t+1} + \gamma \sum \limits_{s’\in S} P^a_{ss’} v_\pi(s’)$

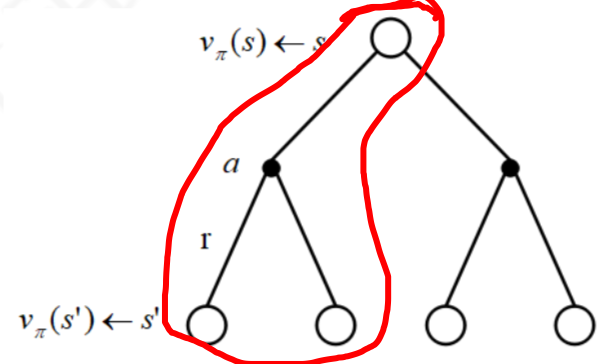
是按照期望展开，就是把所有可能采取的动作action，都按照概率p和对应过去的状态s’的价值，sum到一起，恩，就是期望的公式。对，仔细看，后面是$v(s’)$，$q(s,a)$就是“把后续的可能的$v(s’)$期望到了一起”！

看上图，看出来了吧，就一半。也就是$v(s)$由$q(s,a1)$和$q(s,a1)$组成，当然不是简单相加，而且按照概率求期望，所以，这就引出了$q(s,a1)$和$v(s)$的关系：

$v_\pi(s) = \sum \limits_{a\in A} \pi(a|s) q_\pi(s,a)$

然后，我把$q_\pi(s,a)$用上面的式子，带入，得到：

$v_\pi(s) = \sum \limits_{a\in A} \pi(a|s) \left( R_s^a + \gamma \sum\limits_{s’\in S} P^a_{ss’} v_\pi(s’) \right)$

同样的推导，$v(s)$带入到$q_\pi(s,a)$中，得到更详细的$q_\pi(s,a)$:

$q_\pi(s,a) = R_s^a + \gamma \sum \limits_{s\in S} P^a_{ss’} \sum\limits_{a’\in A} \pi(a’|s’) q_\pi(s’,a’)$

这一通骚操作，都晕了吧，没事，你感兴趣推导，就自己去看叶欣的《强化学习》$p_{12} - p_{13}$去，其实，这一通操作，就是想表达，价值函数和动作函数之间的是$\sum$期望的关系，你捋顺他们的关系，就容易懂了。

值函数$v(s)$、行为函数$q(s,a)$的作用

前面说了一堆，回顾一下，啥贝尔曼方程，啥状态价值，啥行为价值。贝尔曼方程，揭示了，当前状态的价值，可以由后续的状态价值递归退出来；从而进一步推导出来，状态价值可以由后续的状态价值求出，也可以由后续的所有的行为价值求出；同理，行为价值又由后续的行为价值求出，也可以由后续的所有的状态价值求出。

恩，然后呢，然后这些关系我搞清楚，我要用学到的这些本事干啥？

求策略啊！！！你丫千万别忘了，我们终极目标，是要找到一个牛逼的策略$\pi$啊。有了$\pi$，我们才可以$a=\pi(s)$，或者由联合概率$\pi(a|s)$，找到最好的动作action。是滴！行为action，不是石头缝是蹦出来的，而是$\pi$生出来的。

好来，来说说，如何用值函数$v(s)$来评估一个策略牛逼否？

即使假设状态空间 S 和动作空间 A 都是离散且有限，我们还有个帮助我们决定用哪个动作action的策略$\pi$，策略空间也为$|A|^{|S|}$，可能会很大。策略$\pi$在这种离散情况下，其实就是一个映射表，从某个s->a。所以策略空间是一个排列组合的关系。（别忘了，是离散+有限情况下）

值函数可以看作是$\color{red}{对策略π的评估}$。如果在状态s，有一个动作a使得$Q_π(s,a) > V_π(s)$，说明执行动作a比当前的策略$π(a|s)$要好，我们就可以调整参数使得策略 $π(a|s)$ 的$\color{red}{概率增加}$。

如果我一调整我的策略，让我某状态的状态价值函数$v(s)$变大了，那我就应该坚定不移的调整我的策略，让其达到最优。然后我让所有的状态，每个人，都达到他(状态)的最大状态价值，这时候，我一通骚操作后的策略，就是最优策略了啊！！！

最优状态价值函数、最优行为价值函数

解决强化学习问题意味着要寻找一个最优的策略让个体在与环境交互过程中获得始终比其 它策略都要多的收获，这个最优策略用 $\pi_$表示。一旦找到这个最优策略$\pi_$，那么就意味着该强 化学习问题得到了解决。寻找最优策略是一件比较困难的事情，但是可以通过比较两个不同策略 的优劣来确定一个较好的策略。

所以，引出了“最优状态价值函数、最优行为价值函数”概念：

定义:最优状态价值函数[optimal value function]是所有策略下产生的众多状态价值函数 中的最大者:

$v_*(s) = \max\limits_\pi v_\pi(s)$

我理解：就是对某一个状态$s$，他在某个这策略$\pi$下，$v(s)$都比别的策略$\p$最大。

定义:最优行为价值函数[optimal action-value function]是所有策略下产生的众多行为价 值函数中的最大者:

$q_*(s,a) = \max\limits_\pi q_\pi(s,a)$

我理解：还是对某一个给定状态$s$,恰好某个策略$\pi$使得，正在特定的动作$a$上得到的$q(s,a)$最大

定义:策略$\pi$ 优于 $\pi’(\pi\ge\pi’)$，如果对于有限状态集里的任意一个状态s，不等式:$v_{\pi(s)}\ge v_{\pi’}(s)$ 成立。注意！是在$\color{red}{每个状态S}$上，好策略比旧策略的价值函数值$\color{red}都$大！

我理解：啥叫我（策略$\pi$）比你$(\pi’)$好，是我对每个状态的$v_\pi(s)$，都比你给出的$v_\pi’(s)$大

有个结论：（据说不好证明，只要知道结论就成了）

对于任何马尔科夫决策过程，存在一个最优策略 $\pi_*$优于或至少不差于所有其它策略。一个马尔科夫决策过程可能存在不止一个最优策略，但最优策略下的状态价值函数均等同于最优状态价值函数:$v^\pi_* (s) = v_*(s)$;最优策略下的行为价值函数均等同于最优行为价值函数$q^\pi_* (s,a) = q_*(s,a)$。

这话听着好绕口，说的是啥呢？

说的是，可能有多个最优策略，恩，可能有。但是，这些最优策略，最后施加到我们的游戏中，使得最后的每个s的最大状态价值$v_*(s)$，他们都是一样的。也就是$v_{\pi 1}(s)=v_{\pi 2}(s)=v_*(s)$

那，这话有啥用呢？

有用，有大用！就是你找到的最大的$v_*$的时候，那个时刻，对应的就是$v^\pi_*$，就能找到最好的$\pi$了呀。（*表示最大） 而$\pi$实际上是对应的$\color{red}{每一个s}$呀，每一个s的$V(s)$都是最大，而，每一个$V(s)$又应该是这个s下对应的所有的action:a，里面最好的那一个。 那么， 你每次只要去找每个状态s下，最好的那个action:a。每个s下都找到了最优的a，那整个最优策略$\pi$不就相当于找到么！大概就是这么一个思路。这叫啥？值迭代？

我靠，这句话太重要了$\color{red}{最优策略下的行为价值函数均等同于最优行为价值函数q^\pi_* (s,a) = q_*(s,a)}$

这句话说完了，你丫应该敏锐的意识到，我要是能得到一个所有的最优行为价值函数，也就是每个s和a的$q_*(s,a)$，注意哈，这个最优行为价值函数$q_*(s,a)$是没有策略$\pi$啥事的，它是指所有的$\pi$中最大的$q(s,a)$值。然后，然后，来了哈，你就在某个s的时候，就选这个s对应$q_*(s,a)$的那个a，也就是$argmax q(s,a)$的那个a（为何？靠，这个就是$q_*(s,a)$的定义啊），你选这样的a。再重复一遍，你看到某个s，就选丫$q_*(s,a)$对应的a，对，换一个s，你再这么选a，对，如此这般，这尼玛就是一个策略$\pi$呀。而且这个策略就是最优策略$\pi_*$啊。

总结一下，前提是你有了所有的最优行为价值函数，然后看每个状态s，这个s对应的所有的他可能的a，都会有$q(s,a)$，每个$q(s,a)$都会找到一个$q_*(s,a)$，然你$(s)$看一下，那个a对应的$q_*(s,a)$最大，那么这个s，就对应选这个a，每个s都这么干一遍，得到的就是最优策略。这个就是最优策略获得方法。

再絮叨一下，这里的$q_(s,a)$求了2次最大，一次是先找到$q_*(s,a)$，第二次是确定策略a的时候，又被用了一次，找到最大的$q_*(s,a)$对应的a。

那，如何用数学表达这个最优策略$\pi_*$呢?

\[\pi_*(a\|s) = \left\{ \begin{align} \label{最优策略确定方法} 1 & \text{ 如果 } \arg\max\limits_{a \in A} q_\*(s,a) \\ 0 & \text{ 其他情况} \end{align} \right.\]

成嘞!

所以，找最优策略$\pi_*$这事，就变成了求解最优行为价值函数$q_*(s,a)$的问题了。

好，我们继续，那我们，如何求出最优行为价值函数$q_*(s,a)$呢？

我们先回顾一下贝尔曼方程：

$v_\pi(s) = \sum\limits_{a\in A} \pi(a|s) q_\pi(s,a)$

ok，那我把最优策略$\pi_*$，带入到这个方程中，得到贝尔曼最优方程（原来就是把最优策略$\pi_*$带入进去就得到了啊，我之前还发愁怎么推导贝尔曼最优方程呢）

$v_\pi^*(s) = \sum\limits_{a\in A} \pi^*(a|s) q_\pi^*(s,a)$

$q_\pi^*(s,a) = R_s^a + \gamma \sum\limits_{s\in S} P^a_{ss’} v_*(s’)$

由于，我们采用上述说的那个方法选择出最优策略的，所以，只有$q_*(s,a)$最大的那个a的概率是1，其他的都是0，所以上述式子就变成了：

$v_\pi^*(s) = \max\limits_a q_\pi^*(s,a)$ ===> 注意哈：这个前提是采用了上面的最优策略确定方法才可以推出

然后，就可以继续推导出：

$v_*(s) = \max \limits_a ( R_s^a + \gamma \sum\limits_{s\in S} P^a_{ss’} v_*(s’))$

$q_*(s,a) = R_s^a + \gamma \sum\limits_{s\in S} P^a_{ss’} \max\limits_{a’} q_*(s’,a’)$

某状态的最优价值等同于该状态下所有的行为价值中最大者，某一行为的最优行 为价值可以由该行为可能进入的所有后续状态的最优状态价值来计算得到。

贝尔曼最优方程不是线性方程，无法直接求解，通常采用迭代法来求解，具体有价值迭代、 策略迭代、Q 学习、Sarsa 学习等多种迭代方法，后续几章将陆续介绍。

对，我们就是要求 最优行为价值函数$q_*(s,a)$ , 这是我们的目标，后续就会用各种方法来求它。

策略迭代

从任意一个状态价值函数开始，依据给定的策略，结合贝尔曼期望方程、状态转移概率和奖励同步迭代更新状态价值函数，直至其收敛，得到该策略下最 终的状态价值函数。理解该算法的关键在于在一个迭代周期内如何更新每一个状态的价值。

依据新的策略 $\pi’$会得到一个新的价值函数，并产生新的贪婪策略，如此重复循环迭代将最 终得到最优价值函数 $v_∗$ 和最优策略 $\pi_*$。

从一个初始策略$\pi$和初始价值函数$v(s)$开始，基于该策略进行完整的价值评估过程得到一个新的价值函数，随后依据新的价值函数得到新的贪心策略，随后计算新的贪婪策略下的价值函数，整个过程反复进行，在这个循环过程中$\color{red}{策略和价值函数均得到迭代更新}$，并最终收敛值最有价值函数和最优策略。除初始策略外，迭代中的策略均是依据价值函数的贪婪策略。

例子

下图是一个叫Small Gridworld的例子，左上角和右下角是终点，$\gamma$=1，移动一步reward减少1，起始的random policy是朝每个能走的方向概率相同，先单独看左边一列，它表示在第k次迭代每个state上value function的值，这一列始终采用了random policy，这里的value function就是通过Bellman Expectation Equation得到的。而右边一列就是在当前的value function情况下通过greedy算法找到当前朝哪个方向走更好。

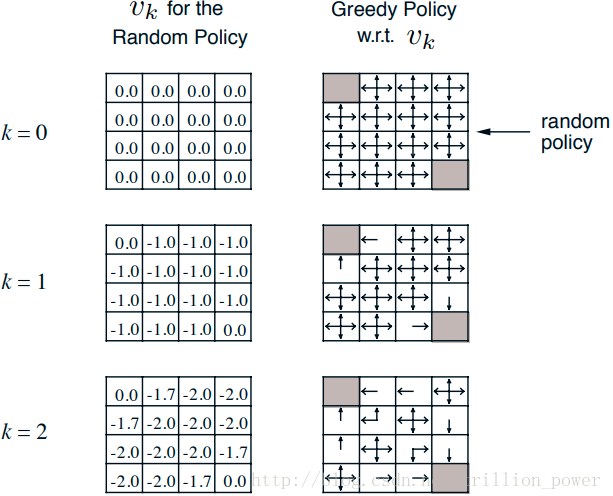
策略评估就是计算任意策略的状态值函数$V_π$，也就是对当前策略下计算出每个状态下的状态值，这就是策略预估，我们也把它称为预测问题。他的计算方式参考之前我们提到过得状态值函数。

$V_\pi(s) = E_\pi[G_t|S_t=s]$

$V_\pi(s) = E_\pi[R_{t+1}+\gamma G_{t+1}|S_t=s]$

$V_\pi(s) = E_\pi[R_{t+1}+\gamma V(S_{t+1})|S_t=s]$

$V_\pi(s) = \sum_a\pi(a|s)\sum_{s’}P(s’|s,a)(R(s,a,s′)+γV_\pi(s′))$

因为是策略迭代所以此处的π(a|s)即为在 s 状态下选取 a 动作的可能，所以策略迭代的公式应该为

$V_{k+1}(s) = \sum_a\pi(a|s)\sum_{s’,r}P(s’,r|s,a)(r+γV_k(s′))$

$\color{blue}{算一算v([1,1]),k=1}$

看这个，k=2，s=[1,2]，就是那个“-1”是咋来的？

参考这个公式：

$V_{k+1}(s) = \sum_a\pi(a|s)\sum_{s’,r}P(s’,r|s,a)(r+\gamma V_k(s′))$

在我们这个例子里，pi(a|s)是1/4=0.25，也就是往每个方向都是0.25的概率。P(s’,r|s,a)始终是1，因为我们这个例子中，一旦s,a给定了，他100%会跳到对应的状态上去；另外，$\gamma=1$。所以上式简化成：

$V_{k+1}(s) = \sum_a 0.25 (r+ V_k(s′))$

好，用这个式子，我们算k=1的[1,2]的$v(s)$把：

每当个体采取了一个行为后，只要这个行为是 个体在非终止状态时执行的，不管个体随后到达哪一个状态，环境都将给予个体值为 −1 的奖励 值;

无论是终态是不是终点，都给reward为-1，我之前以为，如果下一步是那2个终点就给奖励0呢，所以怎么算都算不对。

$v[1,1]= 0.25(-1+0) + 0.25(-1+0) + 0.25(-1+0) + 0.25(-1+0) = -1$

$\color{blue}{再算一算状态v([1,1]), k=2}$

k2=2时刻，第一行第二列的1.7怎么来的呢？

他的下个状态分别是坐标<1,1>,<1,3>,<2,2>，三个位置:

还是参考这个公式：$V_{k+1}(s) = \sum_a 0.25 (r+ V_k(s′))$

$v[1,1]= 0.25(-1+0) + 0.25(-1-1) + 0.25(-1-1) + 0.25(-1-1) = -1.75$

好，我们会算$v(s)$了，我们接下来要干嘛，改进策略啊!

个体处在任何一个状态 时，将比较所有后续可能的状态的价值，从中选择一个最大价值的状态，再选择能到达这一状态 的行为;

对，就是，你都知道你旁边的4个或者3个的状态的价值了，你就选大的那个啊，“人往高处走，水往低处流”嘛~

这个例子很多都讲：

$\color{red}{策略迭代算法}$ - 引自周志华老师的《西瓜书》和一个博客

俩算法一样的，都列出来，没啥区别，对比着看。

几个细节要说明：

  • 算法分两部分，一个是评估，一个是迭代
  • 评估的停止条件是收敛，周志华老师那个条件是$V=V’$，另外一个的终止条件是$\Delta<\theta$，其实意思都是收敛。所以，叶强的《强化学习》的第3.2节用k=2的图来说明策略改进是非常让人误导的，应该是这个$v(s)$所有的值收敛后，才可以做策略迭代。具体是多少，我也不知道，k=？的时候。
  • 一旦基于当前这个策略$\pi$，你一遍遍的迭代着算，$v(s)$（注意，是对每个状态s）都稳定了，你才从这个稳定的转改值里面，用贪心策略，为每一个s，找一个最优的动作。
  • 啥叫“最优”，又得用贝尔曼方程算一遍，就是里面说的$\pi’(s)=argmax_{a\in A} Q(s,a)$，就是算一下每个动作的$Q(s,a)$值，最大的那个，就是我要的动作a。
  • 那如果有多个a的$Q(s,a)$值都一样，我理解，就都留着，只不过，每个人的概率均等，也就是$p(a|s)$为1/|备选a|。

当给定一个策略 $\pi$时，可以得到基于该策略的价值函数$v_\pi$，基于产生的价值函数可以得到一个贪婪策略$\pi′ = greedy(v_\pi$)。依据新的策略$\pi′$会得到一个新的价值函数，并产生新的贪婪策略，如此重复循环迭代将最 终得到最优价值函数 $v_∗$ 和最优策略 $\pi_*$。策略在循环迭代中得到更新改善的过程称为策略迭代$(policy iteration)$。

为什么会收敛，参考资料叶强的《 强化学习入门——从原理到实践》p36给出证明

价值迭代

如果一个 策略不能在当前状态下产生一个最优行为，或者这个策略在针对当前状态的后续状态时不能产生一个最优行为，那么这个策略就不是最优策略。与价值函数对应起来，可以这样描述最优化原则:一个策略能够获得某状态s的最优价值当且仅当该策略也同时获得状态s所有可能的后续状态s′的最优价值。

Q-learning和策略迭代区别？

Q-learning是

没有模型[Model Free]情况下的策略学习

啥叫没有模型？模型是啥？

模型就是你知道状态转移概率$P_{s->s’}$，以及跳到新状态环境给出的rewards（就是知道给分的规则，你丫从这个s，跳到那个s，会的多少分，或者按照啥概率给你多少分）。 那么有模型，就是你根本不知道这些，游戏对你来说，就是个黑盒子，你只能靠自己去误打误撞去体验。

环境已知和模型已知，不是一个概念吧？ 答：错，两者就是一回事。参见叶强的RL p49页model-free的定义。环境已知就是status转移概率和reward已知。

还记得，我们是要干啥来的么？对！我们是要寻找一个打游戏的最优策略，为了找到这个最优策略，我们就通过定义$G_t$，也就是从一个状态开始的累计rewards，从而进而计算$E(G_t)$，也就是算出$V(s)$呀。现在，我们没有上帝视角，我们就没法动态规划，我们就没法用策略迭代、价值迭代来求解了？怎么办？

有个办法，你采样！你就从一堆的玩的游戏记录里面，找到你感兴趣的那个状态s，然后，看从这个s开始，又玩了很多步，然后嗝屁的$\tau$，然后大量的找到这样的从s开始到嗝屁的，这个多了，平均一下，不就成了期望了么。有了期望，你的$v(s)$不就有了么，然后就可以继续啦。

蒙特卡洛方法

再回想，不间断的回想，我们要干啥来着？我们要寻求一个策略，一个最优策略。为此，我们攥出来一个状态的价值函数$v(S)$，这玩意是一个期望值，玩到游戏哏屁的时候，你的累计reward $G_t$的期望$v(s) = E(G_t0)$。回忆起来了吧。之前，咱们有模型的时候，您呀可以通过状态转移概率、每步系统给你的Rewards规则，你可以通过动态规划啥的方法，来得到每个状态的$v(s)$，现在呢？玩了个菜，你两眼一抹黑，你在这个状态，周边都是黑压压，就跟dota里面，周边都是黑乎乎的未探索的境地，你不知道你动动鼠标会跳到啥状态，也不知道系统怎么给你分。这个时候咋办？

从一个状态$s_0$，我们就是要算$v(s_0)$，咋算？

那就采样呗，啥叫采样？就是你玩呗，玩无数局，每一局你都玩到哏屁，然后记下来每一局的得分，然后你取平均值，大数定律告诉我们，当你趋向于无穷次的时候，这个得分会趋向于他的期望值。

对，就是这么暴力，你说了，我玩不到无数局，没事，尽量多玩把，而且，我们还会修正的。

蒙特卡罗强化学习有如下特点:不依赖状态转移概率，直接从经历过的完整的状态序列中学习，使用的思想就是用平均收获值代替价值。理论上完整的状态序列越多，结果越准确

你玩的过程，每一局，我们叫他一个完整的状态序列 (complete episode)，有些书里用罗马字母$\tau$表示： $s_1,a_1,r_2,s_2,a_2,r_3,….s_t,a_t,r_{t+1} —- \pi$

数学上再来表示一遍：

$G_t=r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + … + \gamma^{T-1}r_T$

$v(s)=E(G_t)$

注意哈，我们都是在一个策略$\pi$下讨论这事呢，别忘了，对，都是在算一个$\pi$下的价值函数，还没顾上找牛逼策略呢。

在大量暴力采样求平均值的过程中，我们有个计算方法：累计更新平均值（increase mean）：

\[\begin{align} &\mu_k = \frac{1}{k} \sum_{j=1}^k x_j \\ & = \frac{1}{k} (x_k + \sum_{j=1}^{k-1} x_j) \\ & = \frac{1}{k} (x_k + (k-1) \mu_{k-1}) \\ & = \mu_{k-1} + \frac{1}{k}(x_k - \mu_{k-1}) \\ \end{align}\]

这个式子，看上去是炫技巧，其实很重要，因为后续的很多方法都跟这个式子有关。再仔细看看这个式子：

  • 新的均值（你也可以理解成为期望值），等于上一次迭代的均值，加上一个，新的值和上一次均值的差的1/k
  • 注意，我们要求的就是均值，这个式子相当于不断的在修正这个均值，依据就是新的得到探索的值$x_k$，换句话，也就是说，你的每一次探索$x_k$，都是在帮你在修正均值。

类比到我们的这个游戏强化学习的场景：

\[\begin{align} &v(s_t) = v(s_t) + \frac{1}{N(s_t)} (G_t - v(s_t)) \\ & = v(s_t) + \alpha (G_t - v(s_t)) \\ \end{align}\]

$\alpha = \frac{1}{N(s_t)}$，这个是假设$N(s_t)$，这个$\alpha$就被认为是一个很小很小的常数了，我不知道，这么搞合理不，不过貌似都这么假设。

恩，这个就是蒙特卡洛，有了所有的状态的价值啦，可是，如何做策略的改进呢？答案是，改不了！靠！对！蒙特卡洛只是用来做价值评估的，不是用来做策略改进的，牢记。

好啦，蒙特卡洛我们搞清楚了，我们继续变态的前进，接下来，我们继续通过变态的，恩，其实也不算变态啦，也都是初中生都可以理解的推导，可以得到一个新的方法，就是“时序差分TD”

时序差分强化学习

时序差分强化学习 (temporal-di erence reinforcement learning, TD 学习)

来，我们来推导一下：

\[\begin{align} & v(s_t) = v(s_t) + \alpha (G_t - v(s_t)) \\ & = v(s_t) + \alpha (r_{t+1} + v(s_{t+1}) - v(s_t)) \\ \end{align}\]

看第二步，其实是我们假设了$G_t = r_{t+1} + v(s_{t+1})$，您说了，能这么假设么？说实话，我也不知道，后来查了一下Sutton的书$P_130 公式(6.3)$，里面有段这个，我觉得大概可以解释：

\[\begin{align} & v_\pi(s) = E_\pi( G_t \| S_t = s) \\ & = E_\pi[ \sum_{k=0}^\infty \gamma^k R_{t+k+1} \| S_t = s] \\ & = E_\pi[ R_{t+1} + \gamma \sum_{k=0}^\infty \gamma^k R_{t+k+2} \| S_t = s] \\ & = E_\pi[ R_{t+1} + \gamma v_\pi(S_{t+1}) \| S_t = s] \\ \end{align}\]

看，这个式子可以看出，在计算$v(s)$，也就是$E_\pi(G_t|S_t=s)$的时候，$G_t$可以看做是$R_{t+1} + \gamma v_\pi(S_{t+1})$

所以，最终，我们得到了TD的公式：

\(\color{blue}{V(S_t) \leftarrow V(S_t) + \alpha (R_{t+1} + \gamma V(S_{t+1}) - V(S_t))}\)

说明一下这个式子：

  • 比蒙特卡洛方法好多了，那个是把整个$\tau$跑完一遍，得到一个$G_t$，然后再平均，去算某个状态的$v(s)$
  • 而我TD可以每步得个分，就可以修正$v(s)$，对，是修正，不是平均，递归修正

不基于模型的策略改进

个体在与环境进行交互时，其实际 交互的行为需要基于一个策略产生。在评估一个状态或行为的价值时，也需要基于一个策略，因 为不同的策略下同一个状态或状态行为对的价值是不同的。我们把用来指导个体产生与环境进 行实际交互行为的策略称为行为策略，把用来评价状态或行为价值的策略或者待优化的策略称 为目标策略。如果个体在学习过程中优化的策略与自己的行为策略是同一个策略时，这种学习方 式称为现时策略学习(on-policy learning)，如果个体在学习过程中优化的策略与自己的行为策略 是不同的策略时，这种学习方式称为借鉴策略学习(off-policy learning)。 模型未知的、基于采样的蒙特卡洛或时序差分学习进行控制是解决中等规模问题的方法。 具体包括：不完全贪婪搜索策略、现时蒙特卡洛控制，现时时序差分学习、属于借鉴学习算法的Q 学习等。

在基于模型的时候，我们可以通过贪心策略去寻找不断可以改进的策略：

\[\pi'(s)= \arg\max\limits_{a\in A}(R_s^a + P^a_{ss'}V(s'))\]

是的！回忆一下，就是$argmax Q(s,a)$，找到对应的a，这样的策略去改进。可是现在，不基于模型（model free）的情况下，我们没有状态迁移概率了啊，$P^a_{ss’}$母鸡啊。

那，咱们对这种不基于模型（model free），改进一下改进策略的方法吧：

\[\pi(a\|s) = \left\{ \begin{aligned} & \frac{\epsilon}{m} + 1 - \epsilon & 如果 a^*= \arg\max\limits_{a\in A} Q(s,a) \\ & \frac{\epsilon}{m} & 其他情况\\ \end{aligned} \right.\]

参考资料

一些概念

概念实在是太多了，列出来：

  • 策略迭代（Policy Iteration）
  • 值迭代 （Value Iteration）
  • 策略梯度（Policy Gradient）
  • 基于模型（Model based）
  • 模型无关（Model free）
  • 探索与开发（Exploreation-Exploitation）
  • 马尔可夫过程（Markov Process）：具备马尔科夫性质的序列$p(s_{t+1}|s_t, … , s_0) = p(s_{t+1}|s_t)$
  • 马尔科夫决策过程（MDP - Markov Decision Process）:在马尔可夫过程中 加入一个额外的变量:动作 a,$p(s_{t+1}|s_t, a_t, · · · , s_0, a_0) = p(s_{t+1}|s_t, a_t)$
  • 确定性策略(Deterministic Policy)：就是张确定的s->a的确定表，当前s，做了某个a，去哪个s’
  • 随机性策略(Stochastic Policy):是个概率，s->a->s’，这个s’不是确定的，是个归一化概率
  • 轨迹(Trajectory)
  • 值函数（Value Function）
  • 状态值函数（V(s)） - V函数
  • 状态-动作值函数（Q(s,a)）- Q函数
  • 动态规划算法
  • 策略评估(policy evaluation)
  • 策略改进(policy improvement)
  • 蒙特卡罗方法
  • 同策略(on policy)
  • 异策略(off policy)
  • 时序差分学习(temporal-difference learning) - TD
  • 贝尔曼方程
  • 贝尔曼最优方程
  • ε-贪心法
  • SARSA算法（State Action Reward State Action，SARSA）
  • Q学习(Q-Learning)算法
  • 深度Q网络(deep Q-networks，DQN)
  • 经验回放(experience replay)
  • 目标网络冻结(freezing target networks)
  • 策略梯度(policy gradient)
  • REINFORCE算法
  • 带基准线的 REINFORCE 算法
  • Actor-Critic 算法
  • A2C算法(Advantage Actor-Critic，A2C)
  • A3C算法(Asynchronous Advantage Actor-Critic，A3C)

书系列

视频资料

别人提供的资源

这些都是别人提供的一些DRL的各类资源汇总：