为什么写这篇文章?
主要是这几个概念太重要了,对机器学习,但是又往往容易混淆,网上的文章散落,少有聚合到一起的,我自己学习过程中,有自己的一些理解。这些,都催生要写一篇把这些概念总结、澄清的文章,留作笔记,也分享给广大机学爱好者。
信息量
$I= log_2(\frac{1}{p(x)})=-log_2(p(x))$ 就是对概率小的编码量就大,概率大的、使用频次高的信息编码大,这样,使得整个信息存储空间最小。所以,I通俗就是编码量,就是不确定性,混乱程度,都是一个意思。
熵
$H(X)=-\sum_xp(x)log_2(p(x))$ 信息量取期望,说白了就是衡量一下这个系统的平均混乱度。熵越大,混乱度越大,越不确定。那个曲线人人都知道,就不画了,熵在$p(x)$取x=0.5时候取得最大为1。
联合熵
$H(X,Y)=-\sum_xp(x,y)log_2(p(x,y))$ 这个没啥好说的,熵的两个随机变量的升级版,呵呵
条件熵
$H(X|Y)=-\sum_{x\in X,y\in Y}p(x,y)log(p(x|y)$ 为何前面是p(x,y),而不是条件概率呢?
可以参考http://blog.csdn.net/xwd18280820053/article/details/70739368的推导
这个条件熵,可以理解为:Y给定后,X的信息熵就被减少了,剩余的这个混乱程度就是这个条件熵。
互信息
$I(X;Y)=\sum_{x\in X,y \in Y}log\frac{p(x,y)}{p(x)p(y)}$ $I(X;Y)=H(X)-H(X|Y)$ 互信息就是,Y这个变量引入后,X变量的熵的减少量。这很容易得出一个结论,如果X,Y是相互独立,那么互信息就是0。
熵、联合熵、条件熵、互信息的关系
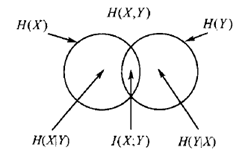
……………………我是分割线…………………..
交叉熵和KL散度和上面的信息熵、互信息和条件熵完全不是一码事,它们都是在谈论1个或者几个随机变量,但是交叉熵和KL散度,谈的则是一个随机变量,但是有多个概率分布,这些概率分布之间的差异大小就是靠KL散度(相对熵)和交叉熵来描述的
关于交叉熵、KL散度参考: http://blog.csdn.net/rtygbwwwerr/article/details/50778098 https://www.zhihu.com/question/65288314/answer/244557337 http://blog.csdn.net/haolexiao/article/details/70142571
交叉熵
$H(p,q)=-\sum_xp(x)logq(x)$ 看!看!只有一个随机变量x,而p,q则是关于x的两种分布
$=\sum_xp(x)log\frac{1}{q(x)}$看!看!这个是拿q来编码p,如果不理解,看最最上面关于信息量的解释
KL散度(相对熵)
$D_{KL}(A||B)=\sum_ip(x_i)log( \frac{p(x_i)}{q(x_i)})$
大白话,就是两种分布的差异性。
信息熵、交叉熵、KL散度的关系
$D_{KL}(A||B)=\sum_ip(x_i)log( \frac{p(x_i)}{q(x_i)})$
$=\sum_ip(x_i)logp(x_i)-\sum_ip(x_i)logq(x_i)$
$=H(p)-H(p,q)$ 看!就是p的信息熵减去p、q的交叉熵呀
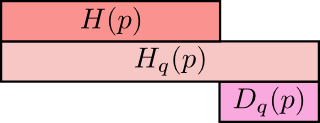
上面是q所含的信息量/平均编码长度H(p) 第二行是cross-entropy,即用q来编码p所含的信息量/平均编码长度|或者称之为q对p的cross-entropy 第三行是上面两者之间的差值即为q对p的KL距离
这里有个问题:为什么机器学习中,都用交叉熵,而不用KL散度?
首先说说,在多分类问题中,往往多个分类中只有一个分类结果为1,其他都为0,(one hot向量的样子)这种结果可以认为是真实概率分布;而用机器学习算法推断出来,比如softmax,往往是一个每个分类上都有归一化的结果的(一个多维度都有值的向量,但是全部相加为1),这种标签结果和机器学出来的记过,可以认为是两种分布,那么就需要一种损失函数,让这两种分布尽量接近,天然的,就看两种分布的相似度,尼玛,这不就是KL最擅长的事么!
但是,为毛又大家都不用KL,反倒用了晦涩难懂的交叉熵呢?
这是因为,丫简单,就酱紫。黑线|||3条… 真不是开玩笑,这点很重要!但是,还是有一些其他原因的。
https://www.zhihu.com/question/65288314/answer/244557337
$D_{KL}(A||B) = -H(A)+H(A,B) $ 如果 $H(A)$是一个常量,那么 $D_{KL}(A||B) = H(A,B)$ ,也就是说KL散度和交叉熵在特定条件下等价。这个发现是这篇回答的重点。 既然等价,那么我们优先选择更简单的公式,因此选择交叉熵。
