序
泰勒展开非常重要,去听妈咪说的讲解,很是有感觉,很想把这些数学概念都柔和到一起。
泰勒展开
由来
为何泰勒要攒出这么一个展开来呢,根本原因是,他想把任何函数,都可以用一堆的多项式来拟合,为何是多项式啊?因为多项式简单啊。
漂亮的解释
妈咪说的解释,真叫是一个赞👍!
他用了一个类比,一个小人很变态的东跑西跳,方向还非常飘忽走位,现在呢,另外一个小人,怎么能完全模拟出这个小人的走位呢?
所以,我们需要有初始的速度,然后还要有一样的加速度,还要有加速度的加速度,还要有加速度的加速度的加速度…,都做到了,这小人跟被模仿的小人的走位一样啦。这就是一个朴素的理解。
而这加速度,加加速度,加加加速度,…,实际上就是1阶导、2阶导、3阶导…,整个模拟过程,就是一个泰勒展开。
严谨的推导
我要用一个多项式$g(x)$来拟合一个函数$f(x)$,我假设,这个多项式$g(x)$长这个样子:
$ f(x) = g(x) = a_o + a_1x + a_2x^2 + a_3x^3 + … + a_nx^n $
好,那我先算算$x=0$的时候吧,
$ f(0) = g(0) = a_o $
然后,我对$g(x),f(x)$都求导后,再求$x=0$的值:
$ f’(0) = g’(0) = a_1 $
再求2阶导,3阶导,…,N阶导
$ f’‘(0) = g’‘(0) = 2a_2 $
$ f’’‘(0) = g’’‘(0) = 3!a_3 $
………
$ f^n(0) = g^n(0) = n!a_n $
好啦,这样就可以求出来$a_o,a_1,…,a_n$了
$a_o=f(0)$
$a_1=\frac{f’(0)}{1!}$
$a_2=\frac{f^2(0)}{2!}$
$a_2=\frac{f^3(0)}{3!}$
……..
$a_n=f^n(0)/n!$
把这个式子带回到多项式表示中,我们得到了著名的“麦克劳林展开式”:
$ f(x) = g(x) = f(0) + \frac{f’(0)}{1!}x + \frac{f^2(0)}{2!}x^2 + \frac{f^3(0)}{3!}x^3 + … + \frac{f^n(0)}{n!}x^n $
看!推导起来,不是很难,是不是。
然后,把麦克劳林展开式从0点的展开,扩展到任意的一个点$a$处,相当于把函数$f(x)$沿着$x$轴方向移动了a个单位,这样就得到了泰勒展开式:
$ f(u) = g(u) = f(u=0) + \frac{f’(u=0)}{1!}x + \frac{f^2(0)}{2!}x^2 + \frac{f^3(0)}{3!}x^3 + … + \frac{f^n(0)}{n!}x^n $
好,说完泰勒展开,说说欧拉公式!
欧拉公式
妈咪说和李永乐老师讲的都很棒,不过都差不多,妈咪说给出了证明。
先说说虚数
虚数单位$i$,他的定义是$i=\sqrt{-1}$,也就是说$i^1=-1$,这个是为了解决实数在开方这个运算上不封闭,而扩展到了复数域,恩,复数域终于封闭了!
复数就可以标示为$a+bi$,$a、b$都为实数,其中$a$叫实部,$b$叫虚部,一个虚数,可以在一个复平面上,用一个向量表示。
$i$有个特性,挺有意思的,就是用它乘以一个复数,就相当于是这个复数对应的向量,逆时针旋转$90^{\circ}$。
一个复数,还可以表示生成三角函数:$a(cos\theta + i*sin\theta)$,介就把复数,表示成了一个极坐标,酷吧。
这个$a(cos\theta + i*sin\theta)$如果套入到欧拉公式($a(cos\theta + i*sin\theta) = e^{i\theta}$),复数就变成了$e^{i\theta}$了。(欧拉公式我们回头再证明,先给出,主要是想说明,复数的多种表示形式),当$\theta=\pi$的时候,导入到欧拉公式,就是著名的欧拉恒等式($e^{i\pi}=-1$)么?哈哈,酷。
欧拉公式
先说说3个函数$e^x,cos(x),sin(x)$的麦克劳林展开式:
\[\begin{align} e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...+\frac{x^n}{n!} \\ cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}+... \tag{1} \\ sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}+... \tag{2} \\ \end{align}\]那么,我们把x换成一个虚数$x=i\theta$,带入到展开式中:
$e^{i\theta}=1+i\theta+\frac{(i\theta)^2}{2!}+\frac{(i\theta)^3}{3!}+\frac{(i\theta)^4}{4!}+\frac{(i\theta)^5}{5!}+\frac{(i\theta)^6}{6!}+\frac{(i\theta)^7}{7!}+…+\frac{(i\theta)^n}{n!}$
我们知道$i^2=-1,i^4=1$,这样式子就成了:
$e^{i\theta}=1+i\theta-\frac{\theta^2}{2!}-\frac{\theta^3}{3!}i+\frac{\theta^4}{4!}+\frac{\theta^5}{5!}i-\frac{\theta^6}{6!}-\frac{\theta^7}{7!}i+…$
我们合并一下实部和虚部:
$e^{i\theta}=(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\frac{\theta^6}{6!}+…) + (\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+…)i$
发现了么?参考上面的麦克劳林展开式$(1)和(2)$,实部恰好是$cos\theta$,虚部恰好是$sin\theta$,所以,最终我们得到了欧拉公式:
\(e^{i\theta}=cos(\theta)+sin(\theta)i\)
欧拉恒等式
前面已经提过了,当$\theta=\pi$的时候,欧拉公式就变成了:
$\color{red}{e^{i\pi}+1=0}$
这就是数学上所谓的最美恒等式,包含了数学里面最神秘和常见的几个元素:$1,i,e,0,\pi$
傅里叶变换
傅里叶级数:任何一个周期函数,都可以写成一系列正弦、余弦函数的组合。
每个正弦、余弦函数还要包含几个参数:
- 振幅
- 频率
- 相位
但是,傅里叶级数的分解,是要求函数得是周期函数,但是,如果不是周期函数,那咋样?
那就要靠傅里叶变换了(也叫连续傅里叶变换)
三角函数正交性
为何要推导“三角函数正交性”?这是为了表达,1,sin,cos是一组在频域中的标准正交基,这样, 一个函数的,可以分解成傅里叶级数,也就可以看成是这3个标准正交基的线性组合了。 我们知道,任何一个向量,都可以看成是一个此空间下的标准正交基的线性组合,就是为了满足这个变态的要求。
三角函数积化和差公式
参考知乎三角函数推导
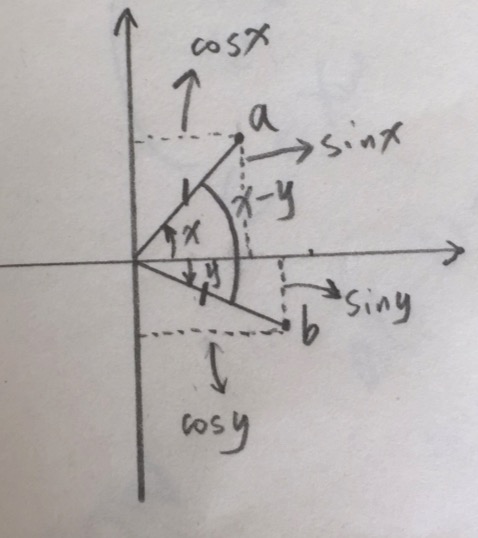
看上图,俩向量$a,b$,我们假设,$a,b$的模都是1,这样,就得到了a,b两点的向量表示:
$a:(cosx,sinx)$
$b:(cosy,siny)$
然后我们做$a,b$点积:
$ a \cdot b = |a|*|b|*cos(\theta)$
其中,$\theta$是$a,b$两向量之间的夹角。$\theta=x-y$(注意,角度一个是正,一个是负,所以要相减,才可以得到夹角)
所以,可以推出:
$cos(x-y)=cosx*cosy + sinx*siny$ (1)
把$y=-y$,带入上式,得到:
$cos(x+y)=cosx*cosy - sinx*siny$ (2)
把$x=\frac{\pi}{2}-x$,带入上式,得到:
$sin(x+y)=sinx*cosy + cosx*siny$ (3)
把$y=-y$,带入上式,得到:
$sin(x-y)=sinx*cosy - cosx*siny$ (4)
(1)和(2)相减,就可以得到,积化和差公式:
$sin(x)*sin(y) = \frac{1}{2}[cos(x-y) - cos(x+y)]$
(3)和(4)相加,就可以得到,积化和差公式:
$sin(x)*cos(y) = \frac{1}{2}[sin(x-y) + sin(x+y)]$
正交性证明
\[\begin{align} & \int_{-\pi}^\pi sinmx * cosnx dx \\ = & \frac{1}{2}\left[ \int_{-\pi}^\pi sin(n+m)xdx + \int_{-\pi}^\pi sin(n-m)xdx \right] \\ = & -\frac{1}{2}\left[ \frac{1}{n+m} cos(n+m) x|_{-\pi}^\pi + \frac{1}{n+m} cos(n-m) x|_{-\pi}^\pi \right]\\ = & 0 \end{align}\]类似的,可以证明:
\[\int_{-\pi}^\pi sinmx * sinnx dx = \left\{ \begin{aligned} 0,&m\neq n \\ \pi,&m=n \neq 0 \end{aligned} \right.\] \[\int_{-\pi}^\pi cosmx * cosnx dx = \left\{ \begin{aligned} 0,&m\neq n \\ \pi,&m=n \neq 0 \end{aligned} \right.\]傅里叶级数
https://zhuanlan.zhihu.com/p/41455378
傅里叶猜想
首先啊,傅里叶猜,是不是任何一个周期函数,可以考虑变成一堆的$sin,cos$函数的叠加?
形如,
$f(t)=a_0+\sum_{n=1}^\infty A_n * sin(nt+\phi)$
然后,可以推导:
\[\begin{align} f(t) & =a_0+\sum_{n=1}^\infty A_n * sin(nt+\phi)\\ & =a_0+\sum_{n=1}^\infty A_n * (sin(\phi) * cos(nt) + cos(\phi) * sin(nt)) \tag{5} \\ & =a_0+\sum_{n=1}^\infty (a_n * sin(\phi)) * cos(nt) + (a_n * cos(\phi) * sin(nt) \\ & =a_0+\sum_{n=1}^\infty a_n * cos(nt) + b_n * sin(nt) \end{align}\]其中式(5)是利用了三角公式(3)。最终,我们得到傅里叶级数的这个样子:
$f(t)= a_0 + \sum_{n=1}^\infty a_n * cos(nt) + \sum_{n=1}^\infty b_n * sin(nt)$ (6)
我们,对他两边积分:
$\int_{-\pi}^{\pi}f(t) dt= \int_{-\pi}^{\pi}a_0 dt + \sum_{n=1}^\infty a_n * \int_{-\pi}^{\pi}cos(nt)dt + \sum_{n=1}^\infty b_n * \int_{-\pi}^{\pi}sin(nt)dt$
后面两项三角函数积分为0,
所以,我们得到 $a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(t) dt$
然后,我们再在(6)式上,左右都乘以$coskt$,我们得到: $\int_{-\pi}^{\pi}f(t)coskt dt= \int_{-\pi}^{\pi}a_0 coskt dt + \sum_{n=1}^\infty a_n * \int_{-\pi}^{\pi}cos(nt)cos(kt)dt + \sum_{n=1}^\infty b_n * \int_{-\pi}^{\pi}sin(nt)cos(kt)dt$
第1项积分为0,第3项根据上面正交性的第一项恒等0,就剩下第2项了:
$\int_{-\pi}^{\pi}f(t)coskt dt= \sum_{n=1}^\infty a_n * \int_{-\pi}^{\pi}cos(nt)cos(kt)dt$
然后,由之前的证明过的三角正交性,当$k=n$时候,这项为0,当$k \neq n$时候,这项为$\pi$,最终,我们得到了:
$\int_{-\pi}^{\pi}f(t)coskt dt= a_k\pi$
所以,我们终于得到一个通项$a_k$的求法:
$a_k=\frac{1}{\pi}\int_{-\pi}^{\pi}f(t)coskt dt$
同理,我们可得:
$b_k=\frac{1}{\pi}\int_{-\pi}^{\pi}f(t)sinkt dt$
这样,我们就得到2个通项:$a_k,b_k$
