EM算法的一些思考
EM 算法是 Dempster,Laind,Rubin 于 1977 年提出的求参数极大似然估计的一种方法。EM算法其实更准确说是一个方法论,是一种计算的方法。卧槽,这个算法都41年了!学机器学习把,多复古,多有生命力啊,顺道吐槽一下。
EM用于啥情况啥问题的解决呢?他要解决啥呢? 他要解决的就是A.隐变量存在,未知、B.参数未知,我靠,俩都未知,咋办。 比如我判断3个高斯按照某种比例分布,但是比例多少不知道,3个高斯的参数均值和方差也未知。 再比如我有3骰子,我置了第一个骰子单双号再决定置第二个骰子,比如单号置剩余的A号骰子,双号置剩余的B号骰子,最终得到一个骰子序列,而这些骰子的某个面的概率不等,让你推断第一个决定单双号的骰子单双号的概率,和后面2个骰子各个面的概率。
真够变态的!这些玩法!
两种学习方法:
- 欧拉方法
- 高斯方法:太严格,晦涩。
EM算法和GMM:
- EM是算法,
- GMM是模型,实打实可以用的东西,是算法推导的结果。
唉,有时候,把问题说清楚、能提出合适的问题,本身就是一件难事。
EM的资料我学习过程中,使用了
- 自然语言处理-序列模型-小象学院-史老师 CRF部分提到EM
- 李航老师的《统计学习方法》第9章
- 《PRML》的第9.4节
- 徐亦达|概率机器学习|高阶讲解
- 邹博的小象的课 EM
- 一个老外讲的,很清晰
- 网上的不错的文章
但是,还是稀里糊涂的,之前听过,想过,都半截放弃掉了,这次痛下决心,一定搞清楚。
先说说对EM的理解:
无论是李航的推导,还是AndrewNG的推导,都是在构建一个对数似然函数,来求$\theta$,但是有隐变量$Z$的存在,所以,就利用Jensen不等式,生生构建出一个函数来,这个函数是对数似然函数的下界,大白话就是总是比似然函数要低。
有了这个下届函数,导出Q函数,Q函数和下届函数等价,这个Q函数是包含了未知参数$\theta$的,然后假装这个$\theta$已知(上来胡蒙一个,之后就靠EM的M阶段推导出来了),然后得到一个关于一个$\mu$或者$\gamma$。$\mu$和$\gamma$的推导定义,参考李航书$P_{156}$和$P_{165}$
$\mu$或者$\gamma$都是期望值,啥叫期望值,是统计的概念,是$\sum$样本 * 概率分布的,所以每拨的样本就做一次期望计算,比如扔抛硬币那个例子里,抛了5次,其中第一次是5个上5个下,那么这次关于隐变量$\mu$期望值($\mu$)代表是隐含的A朝上的次数,再次提醒)就是

其实,我一直不太明白,这个$\mu$或者$\gamma$是怎么推出来的,上面说到的李航书里给出了,但是没有说为什么就是这个式子?!我觉得李航根本没给出这个东西的说明,而且邹博的讲解里也没给出,唯一见到的就是这篇文章中,说“因为他是伯努利分布….”,所以就balabala:

另外,在看看正太分布那个例子中的对于$\gamma$的概率计算,也是大概这个样子,
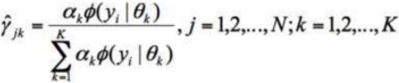
看到了把,分子是这次(第j个样本)的来自某个(第k个分布)的概率,或者第j个样本,来自A钱币朝上的概率。分母呢,是一个归一化的汇总,比如所有的来自各个分布概率的汇总,或者是来自A朝上和朝下的概率的汇总。挺像的吧,感觉就是个归一化似得,但是我是觉得,这个绝不是偶然,一定是某种推导的结果,但是没有找到任何文献或者文章描述这个细节???
下届函数
这个函数,李航的推导的是$B(\theta,\theta^{(i)})$ ,还是AndrewNG的推导的$J(Q,\theta)$,
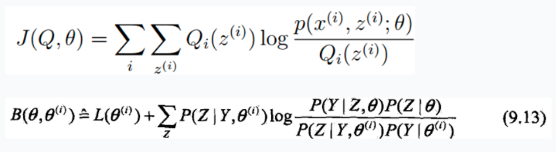
Q函数
Q函数的引入
李航老师的书中,然后,推导出,假设当前$\theta_i$已知,推导出让这个下界函数(B函数)取得最大值的时候,下一个$\theta_{i+1}$该取得值。推导过程中 ,就推出了Q函数,

定义9.1:(Q函数)完全数据的对数似然函数$logP(Y,Z|\theta)$, 关于在给定的观测数据Y和当前参数$\theta^{(i)}$下,对未观测数据$Z$的条件概率分布$P(Z|Y,\theta^{(i)})$的期望,称为Q函数。 (《统计学习方法》$P_{158}$页) 这个定义狠诡异,是$logP(Y,Z|\theta)$
AndrewNG的Q函数是生凑出来的,它表示Z在假设$\theta$给定后,Z的概率分布函数。(这个和李航老师的Z的分布的期望值的那个定义,还是有很大的差别的)
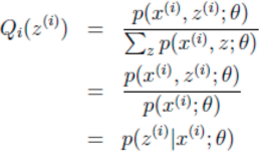
但是,殊途同归,最终都推导出Q函数,Q函数是EM算法的核心!
两者区别是,李航的Q函数是一个关于Z的期望,而AndrewNG的是一个概率分布。 不过无所谓,都可以用来推导后续的东西,为什么叫后续推导呢?因为针对不同的分布,推倒的方式就是不同的了。 比如Z的分布和Y的分布都是伯努利分布,那对应的这个文章中抛硬币的例子,如果是Z是一个多项分布,Y是一个正态分布,那么就对应这个文章中的男女生分布的例子。
引自《PRML》
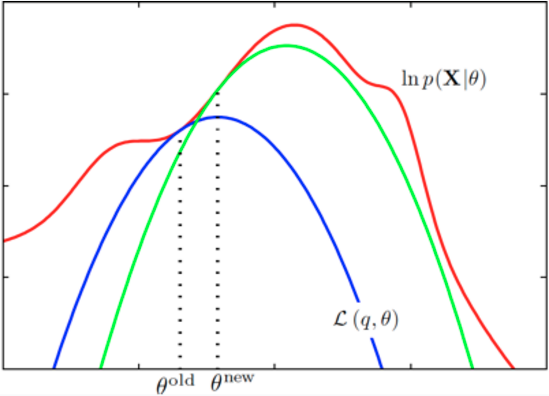
更⼩的下届,它的值等于在旧处的对数似然函数值,⽤蓝⾊曲线表⽰。注意,下界与对数似然函数在旧处以切线的⽅式连接,因此两条曲线的梯度相同。这个界是⼀个凹函数,对于指数族分布的混合分布来说,有唯⼀的最⼤值。在M步骤中,下界被最⼤化,得到了新的值新,这个值给出了⽐旧处更⼤的对数似然函数值。接下来的E步骤构建了⼀个新的下界,它在新处与对数似然函数切线连接,⽤绿⾊曲线表⽰。
这个绿线、蓝线就是李航老师讲的$B(\theta,\theta^{(i)})$函数(《统计学习方法》$P_{159}$页)
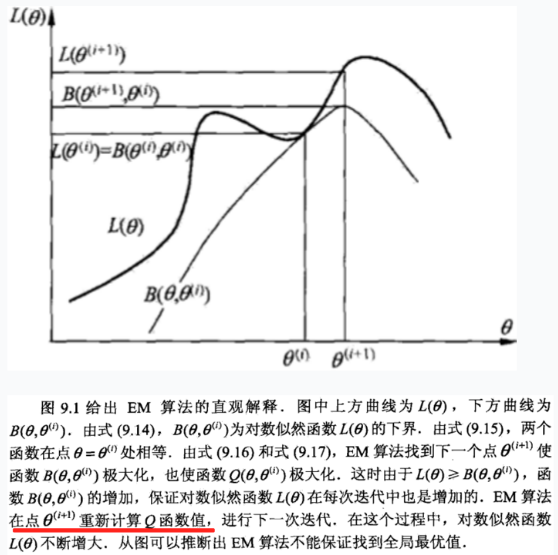
上面摘抄了2本书的这个逼近曲线,大致就是说,$L(\theta)$咱不是不好算么,那么我就用$Q(\theta,\theta_i)$逼近,先找个她们俩交界的时候的那个$\theta_i$(这个真心不理解?!为何在这个点,他就是个相交并且是下届呢?!),然后,这个时候,确定了这个Q函数,这个Q函数包含了$\theta$变量,是一个关于$\theta$的函数,然后,对这个函数求最大化,从而得到一个新的最大化Q时候的$\theta$的表达式,这个时候,恰好是可以通过样例数据可以算出来,从而,确定了一组新的$\theta$,然后交替进行,得到最逼近的$L(\theta)$的$\theta$。停止条件,就是$\theta$的这次和上次的距离尽量短。$|\theta_t - \theta_{t+1}|<\epsilon$,或者是Q两次具体某个阈值。
再叨叨几句
EM适合模型中,包含隐含变量Z,这样不太好用样本X去直接似然估计$\theta$的情况,这个时候就利用数学推导上的一个Q函数来逼近L($\theta$)的极值的时候的$\theta$。
具体做的时候,先胡乱初始化$\theta$,然后带入Q函数,得到一个关于隐变量Z的式子,然后对Q函数进行$\theta$的偏导求取,得到新的$\theta$,这个新$\theta$是关于隐变量Z概率分布函数的函数,这个时候,通过数据+上轮的$\theta$可以求出这个Z的概率分布值,有了这个Z概率分布值,就可以退出下一轮迭代用的$\theta$,周而复始。
直到达到某个阈值,停止,酱紫。
上面提到的$\theta$是隐变量的函数,是靠对Q函数求$\theta$偏导得到的式子,具体做某种EM算法推导的时候,具体问题具体写式子推导。
